Stammfunktion F
\(\\\)
Das Integral
\( \quad \displaystyle{\int}_0^{2022} f(x) dx \)
\(\\\)
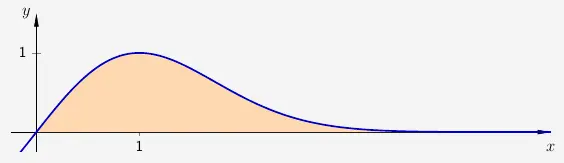
berechnet die Fläche zwischen dem Graphen und der \(x\)-Achse im Intervall \([0;2022]\) .
\(\\\)
\( \quad F(w) - F(0) \)
dagegen berechnet die Fläche zwischen dem Graphen und der \(x\)-Achse im Intervall \([0;w]\), wobei \(w>2022\) ist.
Es liegt die Vermutung nahe, dass die Aussage
\( \quad F(w) - F(0) \; \approx \; \displaystyle{\int}_0^{2022} f(x) dx \)
\(\\\)
wahr ist, denn \(2022\) ist schon ein relativ großer Wert, und \(x \rightarrow \infty\) strebt ja gegen Null. Um das zu überprüfen bestimmen wir \(f(2022)\) mit
\( \quad F(w) - F(0) \; \approx \; \displaystyle{\int}_0^{2022} f(x) dx \)
\(\\\)
Laut Taschenrechner bekommen wir Null heraus, was aber nicht ganz richtig ist. Denn \(f(2022)\) muss oberhalb von Null liegen, da der Graph in dem betreffenden Bereich wie vorher gezeigt streng monoton fallend ist, jedoch keine weiteren Nullstellen als den Koordinatenursprung hat. Jedoch ist der Unterschied so geringfügig, dass er nicht mehr messbar oder mit dem Schultaschenrechner berechenbar ist. Das bedeutet nun, dass \(F(w) - F(0)\) näherungsweise die gleiche Flächengröße hat wie das Integral
\( \quad \displaystyle{\int}_0^{2022} f(x) dx \)
\(\\\)