Funktionen der Schar
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Hochpunkt
Bei \(f_1\) ist \(a=1\) und wir erhalten
\( \quad f_1(x) \; = \; x \cdot e^{-\frac{1}{2} x^2 + \frac{1}{2}} \)
\(\\\)
Wir definieren zunächst die Funktion \(f_1\) als \(f\).
Beachte: Der Mal-Punkt muss bei der Definition mitgeschrieben werden.

\(\\\)
Für Hochpunkte gilt die notwendige Bedingung: \(f_1'(x) =0\)
Wir nutzen für Ableitungen in den mathematischen Vorlagen folgendes Symbol

\(\\\)
und definieren die 1. Ableitung von \(f_1\).

\(\\\)
Die Ableitung lautet nun

\(\\\)
Wir lösen die Gleichung.

\(\\\)
Für Extrempunkte gilt nun die hinreichende Bedingung: \(f_1''(x) \not=0\)
Wir bilden die 2. Ableitung.

\(\\\)
Diese lautet nun

\(\\\)
Wir überprüfen unsere Lösungen.

\(\\\)
Es ist nun
\( \quad \begin{array}{ c c l l } f''(-1) & > & 0 & \quad \Rightarrow \; \textit{Tiefpunkt} \\[6pt] f''(1) & < & 0 & \quad \Rightarrow \; \textit{Hochpunkt} \end{array} \)
\(\\\)
Um den \(y\)-Wert des Hochpunktes zu erhalten, setzen wir \(1\) in die Ausgangsgleichung ein.

\(\\\)
Damit haben wir den Hochpunkt \(H(1|1)\).
\(\\[2em]\)
Aufgabe 2 – Nullstelle und Grenzwert
Für die Nullstelle gilt
\( \quad f(x) \; = \; 0 \)
\(\\\)
Wir lösen die Gleichung.

\(\\\)
Es existiert nur die eine Lösung bei \(x=0\).
Den Grenzwert von \(x \rightarrow \infty\) berechnen wir mit

\(\\\)
Für \(\infty\) verwenden wir die Tastenkombination \(\boxed{ctrl}\) \(\boxed{Buchsymbol}\) :

\(\\\)
Wir geben also Folgendes ein.

\(\\\)
Für \(x \rightarrow + \infty\) strebt \(f_1(x)\) gegen die \(x\)-Achse.
\(\\[2em]\)
Aufgabe 3 – Koordinatenachsen
Wir wissen, dass \(f_1\) nach rechts gegen Null strebt. Wegen der Symmetrie muss die Funktion auch nach links gegen Null streben. Wir kennen auch die Nullstelle bei \(N(0|0)\). Und letzendlich haben wir den Hochpunkt bei \(H(1|1)\). Wegen der Punktsymmetrie ist also der Tiefpunkt bei \(T(-1|-1)\). Daraus folgen die Koordinatenachsen mit der Skalierung.

\(\\[2em]\)
Aufgabe 4 – Stammfunktion
Es gilt
\( \quad F_1(u) - F_1(0) \; = \; \displaystyle{\int}_0^{u} f_1(x) dx \quad \textit{mit} \quad u>2022 \)
\(\\\)
Das heißt nun, dass \(F_1(u) - F_1(0)\) die Integralfläche beschreibt, für die \(u\) größer als \(2022\) ist. Die angegebene Gleichung besagt nun, dass diese Integralfläche nahezu gleich der Integralfläche ist, bei der die obere Grenze genau \(2022\) ist. Daraus folgt, dass für alle \(x\)-Werte über \(2022\) kein oder kaum Zuwachs zur Integralfläche zu erwarten ist. Der Grenzwert
\( \quad \lim \limits_{x \to +\infty} f_1(x) \; = \; 0 \)
\(\\\)
lässt dieses auch vermuten. Und ziehen wir die obige Abbildung hinzu, so ist zu erkennen, dass bereits bei \(x=4\) kaum noch Fläche hinzu kommt.
\(\\[2em]\)
Aufgabe 5 – Steigung und Achsenabschnitt der Geraden
Bei \(f_0\) ist \(a=0\) und wir erhalten
\( \quad \begin{array}{ r c l } f_0(x) & = & x \cdot e^{-\frac{1}{2} \cdot 0 \cdot x^2 + \frac{1}{2}} \\[6pt] & = & x \cdot e^{\frac{1}{2}} \\[6pt] & = & \sqrt{e} \cdot x \\[6pt] & \approx & 1{,}649 x \\ \end{array} \)
\(\\\)
Dieses ist eine Ursprungsgerade von der Form
\( \quad y \; = \; m \cdot x \)
\(\\\)
Ursprungsgerade verlaufen stets durch den Koordinatenursprung \((0|0)\). Die Gerade hat hier die Steigung \(m = \sqrt{e}\).
\(\\[2em]\)
Aufgabe 6 – Parameter a und Winkel
Parameter a
Der Wert von \(a\) wird berechnet, indem \(P(1|e)\) in die Gleichung von \(f_a\) eingesetzt wird.
\( \quad \begin{array}{ r c l l } e & = & 1 \cdot e^{-\frac{1}{2} a \cdot 1^2 + \frac{1}{2}} \\[6pt] e^1 & = & e^{-\frac{1}{2} a + \frac{1}{2}} & \bigl| \, ln\\[6pt] 1 & = & -\frac{1}{2} a + \frac{1}{2} & \bigl| \, -\frac{1}{2} \\[6pt] \frac{1}{2} & = & -\frac{1}{2} a & \bigl| \, : \left(-\frac{1}{2}\right) \\[6pt] -1 & = & a \\ \end{array} \)
\(\\[1em]\)
Winkel an der Stelle x=1
Der Winkel zwischen derParallelen der \(x\)-Achse und der Tangente an den Graphen von \(f_{-1}\)
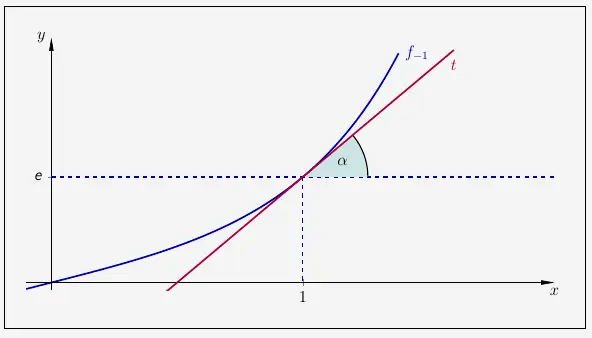
\(\\\)
wird berechnet mit
\( \quad tan (\alpha) \; = \; m \; = \; f'_{-1}(1) \)
\(\\\)
Zunächst bestimmen wir die Steigung \(m\) der Funktionen \(f_{-1}\) an der Stelle \(x=1\). Wir benötigen die Funktion \(f_{-1}\) mit
\( \quad f_{-1}(x) \; = \; x \cdot e^{-\frac{1}{2} \cdot (-1) \cdot x^2 + \frac{1}{2}} \; = \; x \cdot e^{\frac{1}{2} \cdot x^2 + \frac{1}{2}} \)
\(\\\)
Wir definieren diese als Funktion \(g\) :

\(\\\)
Für \(m\) bilden wir die 1. Ableitung

\(\\\)
und berechnen die Steigung an der Stelle \(x=1\).

\(\\\)
Den zu der Steigung gehörenden Steigungswinkel berechnen wir mit der Arkusfunktion des Tangens. Die Arkusfunktion finden wir auf dem CAS unter der Taste \(\boxed{trig}\) :

\(\\\)
Wir berechnen den Winkel mit

\(\\\)Der gesuchte Winkel beträgt ungefähr \(79{,}6^{\circ}\).
\(\\[2em]\)
Aufgabe 7 – Integralflächen
Wegen der Punktsymmetrie sind die Flächen in den Intervallen \([-0{,}5;0]\) und \([0;0{,}5]\) gleich groß, haben jedoch verschiedene Vorzeichen. Daraus folgt
\( \quad \begin{array}{ r c l c l } \displaystyle{\int}_{-0{,}5}^1 f_{-1}(x) dx & = & \underbrace{\displaystyle{\int}_{-0{,}5}^0 f_{-1}(x) dx \; + \; \displaystyle{\int}_0^{0{,}5} f_{-1}(x) dx}_{\text{heben sich gegenseitig auf}} \; + \; \displaystyle{\int}_{0{,}5}^1 f_{-1}(x) dx \\[32pt] \displaystyle{\int}_{-0{,}5}^1 f_{-1}(x) dx & = & \displaystyle{\int}_{0{,}5}^1 f_{-1}(x) dx \\ \end{array} \)
\(\\\)