Karton mit 36 Schachteln
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Drei Schachteln
Ereignis angeben
\(\\\)
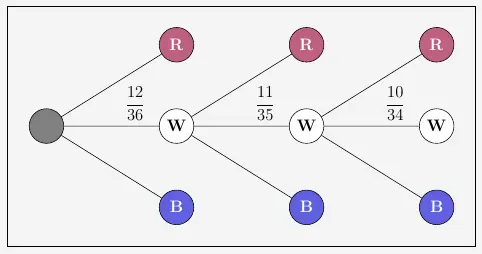
\(\\\)
Wie hier dargestellt ist das Ereignis ,,3-mal weiß‘’ :
\(\quad \frac{12}{36} \cdot \frac{11}{35} \cdot \frac{10}{34} \)
\(\\\) Es könnte aber ebenso gut ,,3-mal rot’‘ oder ,,3-mal blau’‘ sein.
\(\\[1em]\)
Mindestens zweimal weiß
\( \quad \begin{array}{ r c l } P(x \geq 2) & = & P(x=2) + P(x=3) \\[6pt] & = & P(x=2) + \frac{12}{36} \cdot \frac{11}{35} \cdot \frac{10}{34} \\ \end{array} \)
\(\\\)
\(P(x=2)\) kann mit einem Baumdiagramm bestimmt werden oder aber mit der hypergeometrischen Verteilung:
\( \quad \dfrac{\binom{M}{k} \cdot \binom{N-M}{n-k}}{\binom{N}{n}} \)
\(\\\)
Dabei steht
-
der 1. Binomialkoeffizient im Zähler für die Schachteln mit einem weißen Armband,
-
der 2. Binomialkoeffizient im Zähler für die Schachteln mit einem Armband, das nicht weiß ist,
-
der Binomialkoeffizient im Nenner für alle Schachteln.
\(\\\)
Damit ist
\( \quad \begin{array}{ r c l c l c l } P(x=2) & = & \dfrac{\binom{12}{2} \cdot \binom{24}{1}}{ \binom{36}{3}} & = & 0{,}2218 & = & 22{,}18 \, \% \\ \end{array} \)
\(\\\)
und
\( \quad \begin{array}{ r c l } P(x \geq 2) & = & 0{,}2218 + \frac{12}{36} \cdot \frac{11}{35} \cdot \frac{10}{34} \\[8pt] & = & 0{,}2218 + \frac{11}{357} \\[8pt] & = & 0{,}2526 \\[6pt] & = & 25{,}26 \, \% \\ \end{array} \)
\(\\[2em]\)
Aufgabe 2 – Zwei Kartons
Kein weißes Armband
Der Sachverhalt ist in dem folgenden Baumdiagramm mit den Ereignissen
\(\, v\) : Der Karton ist vollständig.
\(\, \overline{v}\) : Der Karton ist nicht vollständig.
\(w\) : Die Schachtel enthält ein weißes Armband.
\(\overline{w}\) : Die Schachtel enthält kein weißes Armband.

\( \quad \begin{array}{ r c l } P(\overline{w}) & = & P(v) \cdot P_v(\overline{w}) + P(\overline{v}) \cdot P_{\overline{v}}(\overline{w}) \\[6pt] & = & \frac{1}{2} \cdot \frac{24}{36} + \frac{1}{2} \cdot \frac{24}{30}\\[6pt] & = & \frac{1}{2} \cdot \frac{2}{3} + \frac{1}{2} \cdot \frac{4}{5}\\[6pt] & = & \frac{11}{15} \\[6pt] & \approx & 0{,}7333 \\[6pt] & = & 73{,}33 \, \% \\ \end{array} \)
\(\\[2em]\)
Bedingte Wahrscheinlichkeit
\( \quad \begin{array}{ r c l } P_w(v) & = & \dfrac{P(v \cap w)}{P(w)} \\[8pt] & = & \dfrac{P(v) \cdot P_v(w)}{1 - P(\overline{w})} \\[8pt] & = & \dfrac{\frac{1}{2} \cdot \frac{1}{3}}{1 - \frac{11}{15}} \\[8pt] & = & \dfrac{5}{8} \\[6pt] & \approx & 0{,}625 \\[6pt] & = & 62{,}5 \, \% \\ \end{array} \)
\(\\\)