Unterzuckerung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Länge des Zeitraums
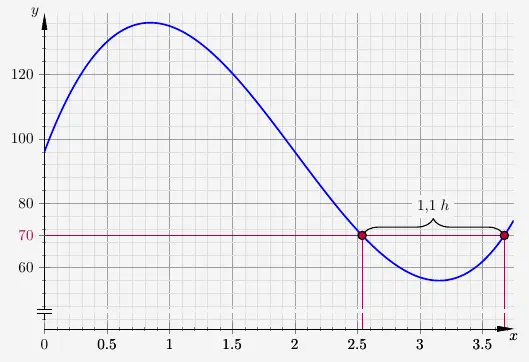
Der Zeitraum beträgt
\( \quad \begin{array}{ r c l } 1{,}1 \; h & = & 1 \; h + 0{,}1 \; h \\[6pt] & = & 1 \; h + 0{,}1 \cdot 60 \; min \\[6pt] & = & 1 \; h \; \; 6 \; min \\\ \end{array} \)
\(\\[2em]\)
Aufgabe 2 – niedrigster Glukosewert
Der niedrigste Glukosewert liegt im lokalen Tiefpunkt der Funktion \(g\). Es gilt die notwendige Bedingung
\( \quad g'(t) \; = \; 0 \)
\(\\\)
Mit der 1. Ableitung
\( \quad g'(t) \; = \; 39 t^2 - 156 t + 104 \)
\(\\\)
ist
\( \quad \begin{array}{ r c l } 0 & = & 39 t^2 - 156 t + 104 \end{array} \)
\(\\\)
Wir lösen dies mit der PQ-Formel oder wie hier mit den Taschenrechnerfunktionen.
\(\\\)
Nach \(\boxed{MENU}\) \(\rightarrow\) \(\boxed{Gleichung/Funkt}\) \(\rightarrow\) \(\boxed{2}\)

\(\\\)
wählen wir \(\boxed{2}\). Wir geben die Parameter ein

\(\\\)
und bestätigen mit \(\boxed{=}\). Wir erhalten

\(\\\)
Mit \(\boxed{S \Leftrightarrow D}\) wird der Wert dezimal angezeigt.

\(\\\)
Wir bestätigen mit \(\boxed{=}\) und lassen uns entsprechend den 2. Wert anzeigen.


\(\\\)
Für Tiefpunkte gilt die hinreichende Bedingung
\( \quad g''(t) \; > \; 0 \)
\(\\\)
Wir überprüfen mit der 2. Ableitung
\( \quad g''(t) \; = \; 78 t - 156 \)
\(\\\)
die berechneten \(t\)-Werte.
\( \quad \begin{array}{ r c c c r } g''\left(\frac{6 + 2 \sqrt{3}}{3}\right) & = & 78 \cdot \frac{6 + 2 \sqrt{3}}{3} - 156 & = & 90{,}06664199 \\[8pt] g''\left(\frac{6 - 2 \sqrt{3}}{3}\right) & = & 78 \cdot \frac{6 - 2 \sqrt{3}}{3} - 156 & = & -90{,}06664199 \\ \end{array} \)
\(\\\)
Damit liegt der Tiefpunkt bei
\( \quad t \; = \; \frac{6 + 2 \sqrt{3}}{3}\; \approx \; 3{,}1547 \)
\(\\\)
Für den \(y\)-Wert setzen wir \(t\) in \(g(t)\) ein:
\( \quad g(t) \; = \; 13 \cdot 3{,}1547^3 - 78 \cdot 3{,}1547^2 + 104 \cdot 3{,}1547 + 96 \; = \; 55{,}97 \)
\(\\\)
Der Tiefpunkt lautet \(T(3{,}15|55{,}97)\).
\(\\[2em]\)
Aufgabe 3 – mehr als 40 Prozent
Wir berechnen die beiden Messwerte.
\( \quad \begin{array}{ r c c c r } g(0) & = & 13 \cdot 0^3 - 78 \cdot 0^2 + 104 \cdot 0 + 96 & = & 96 \\[8pt] g(1) & = & 13 \cdot 1^3 - 78 \cdot 1^2 + 104 \cdot 1 + 96 & = & 135 \\ \end{array} \)
\(\\\)
Wir ermitteln das Verhältnis der beiden Werte zueinander, wobei der Grundwert von \(100\%\) von \(g(0)=96\) gebildet wird.
\( \quad \frac{g(1)}{g(0)} \; = \; \frac{135}{96} \; = \; 1{,}40625 \; = \; 140{,}625\% \)
\(\\\)
Damit liegt der Messwert eine Stunde nach Beginn der Messung um \(40{,}625\%\) höher als zu Beginn der Messung.
\(\\[2em]\)
Aufgabe 4 – Durchschnittswert
Mittelwerte oder auch Durchschnittswerte berechnen wir mit der Formel
\( \quad \overline{m} \; = \; \frac{1}{b-a}\displaystyle{\int}_a^b f(x) dx \)
\(\\\)
Angewendet für \(g(t)\) für die ersten beiden Stunden ergibt
\( \quad \begin{array}{ r c l l } \overline{m} & = & \displaystyle{\int}_0^2 g(t) dt \\[12pt] & = & \frac{1}{2-0} \displaystyle{\int}_0^2 \left(13 \cdot t^3 - 78 \cdot t^2 + 104 \cdot t + 96\right) dt \\[12pt] & = & 122 \\ \end{array} \)
\(\\\)
Graphisch bedeutet das, dass die Größe des grün gefärbten Rechtecks der Größe der schraffierten Fläche unter dem Graphen von \(g\) im Intervall \([0;2]\) entspricht.

\(\\\)