Deichkrone
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Höhe der Deichkrone
Für den Deich, der die Deichkrone erhalten soll, definieren wir eine Funktion \(d\) mit \(k = 5{,}8\).

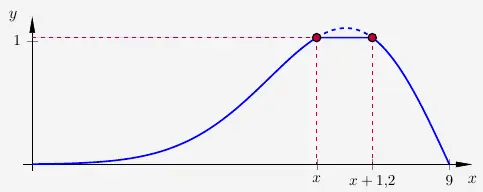
\(\\\)
Zunächst wird \(x\) berechnet.

\(\\\)
Nur \(6{,}136742228\) liegt innerhalb des Definitionsbereichs
\( \quad \mathbb{D} \; = \; \{ x |0 \leq x \leq 9 \} \)
\(\\\)
Ebenfalls liegt
\( \quad 6{,}136742228 + 1{,}2 \; = \; 7{,}336742228 \)
\(\\\)
innerhalb des Definitionsbereichs. Die gesuchte Höhe ergibt sich mit

\(\\\)
Der Deich ist also \(10{,}28 \, m\) hoch.
\(\\[2em]\)
Aufgabe 2 – Neigung des begradigten Bereichs
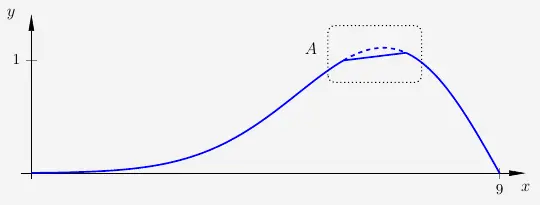
\(\\\)
Die Neigung (von der Landseite aus gesehen) wird mit Hilfe des Steigungsdreiecks berechnet.
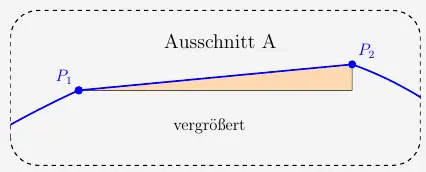
\(\\\)
Es gilt für die Neigung
\( \quad m \; = \; \frac{d(x_2) - d(x_1)}{x_2 - x_1} \)
\(\\\)
Dazu berechnen wir die \(y\)-Werte der Punkte.

\(\\\)
Es ergibt sich die prozentuale Neigung mit
\( \quad \frac{1{,}060715883 - 0{,}9937890337}{7{,}2 - 6} \cdot 100 \% \; = \; 5{,}58 \% \)
\(\\[2em]\)
Aufgabe 3 – Menge des Materials
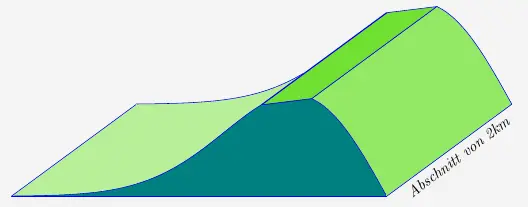
Das benötigte Material entspricht dem Volumen des Deiches und wird berechnet mit
\( \quad V \; = \; \textit{Deichquerschnitt} \cdot \textit{Abschnittslänge} \)
\(\\\)
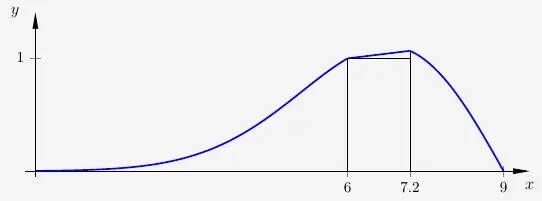
Der Deichquerschnitt kann in drei Teilflächen unterteilt werden:
- der Integralfläche seeseitig bis zur Deichkrone
- der Integralfläche landseitig bis zur Deichkrone
- einem Rechteck unterhalb der Deichkrone mit aufgesetztem Steigungsdreieck
\(\\\)
\(\\\)
Die Teilflächen werden berechnet mit




\(\\\)
Zusammen ergibt sich

\(\\\)
Bei der Querschnittsfläche ist zu beachten, dass sowohl in \(x\)-Richtung als auch in \(y\)-Richtung eine Einheit \(10 \, m\) sind und der Deichabschnitt in \(km\) angegeben ist. Die Rechnung lautet also
\( \quad V \; = \; 4{,}015226081 \cdot 10 \cdot 10 \cdot 2000 \; = \; 803045{,}2162 \, m^3 \)
\(\\\)