Funktionenschar h
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Funktion g liegt nicht in der Schar
Betrachten wir die Funktionenschar \(h_k\) mit
\( \quad \begin{array}{ r c l l } h_k(x) & = & \frac{5}{9}(x - 3)^2 \cdot e^{k(x - 6)} + 4 \end{array} \)
\(\\\)
etwas genauer, so können wir erkennen, dass für \(x=6\) das \(k\) verschwindet. Wir nutzen das aus und berechnen
\( \quad \begin{array}{ r c l l } h_k(6) & = & \frac{5}{9}(6 - 3)^2 \cdot e^{k \cdot (6 - 6)} + 4 \\[12pt] & = & \frac{5}{9} \cdot 9 \cdot e^0 + 4\\[8pt] & = & 5 \cdot 1 + 4\\[6pt] & = & 9 \\ \end{array} \)
\(\\\)
Das bedeutet nun, dass alle Funktionen der Schar durch Punkt \((6|9)\) laufen.
Wie verhält sich das nun bei der Funktion \(g\)?
In der Wertetabelle aus der Aufgabe mit Funktion \(g\) haben wir festgestellt, dass \(g\) durch den Punkt \((6|8{,}95)\) verläuft. Folglich kann die Funktion \(g\) keine Funktion der Schar \(h_k\) sein.
\(\\[2em]\)
Aufgabe 2 – Term
Die Steigung berechnen wir mit der 1. Ableitung.
\( \quad \begin{array}{ r c l l } h_k'(6) & = & \frac{5}{9}(6 - 3) \cdot (6k -3k + 2) \cdot e^{k \cdot (6 - 6)} \\[10pt] & = & \frac{5 \cdot 3}{9} \cdot (3k + 2) \cdot e^0 \\[10pt] & = & \frac{5}{3} \cdot (3k + 2) \\[10pt] & = & \frac{5 \cdot 3k}{3} + \frac{5 \cdot 2}{3} \\[10pt] & = & 5k + \frac{10}{3} \\ \end{array} \)
\(\\[2em]\)
Aufgabe 3 – Innenwinkel von 30°
Der Wert von \(k\) wird über die Tangentensteigung berechnet.
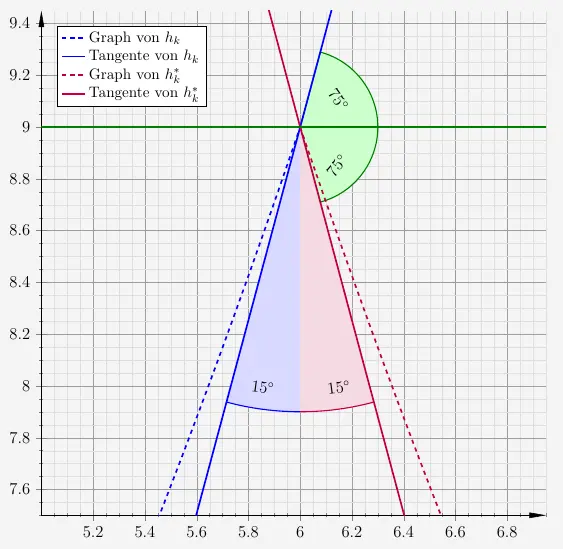
\(\\\)
Haben wir einen Innenwinkel von \(30^\circ\), so hat die Tangente von \(h_k\) an der Stelle \(x=6\) einen Steigungswinkel von \(75^\circ\). Es gilt
\( \quad \begin{array}{ r c l} tan(\alpha) & = & h_k'(6) \end{array} \)
\(\\\)
Mit der vorherigen Aufgabe erhalten wir dann
\( \quad \begin{array}{ r c l l } tan(75^\circ) & = & 5k + \frac{10}{3} & | - \frac{10}{3} \\[10pt] tan(75^\circ) - \frac{10}{3} & = & 5k & | : 5 \\[12pt] \frac{tan(75^\circ) - \frac{10}{3}}{5} & = & k \\[12pt] k & \approx & 0{,}0797 \\ \end{array} \)
\(\\\)