Abbildungen
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Aussage
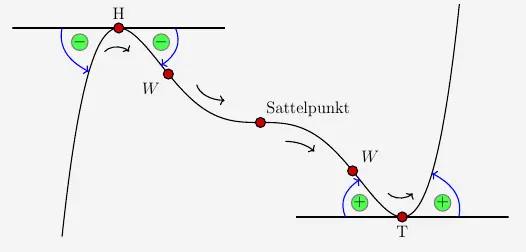
Die 2. Ableitung beschreibt die Krümmung eines Graphen an einer bestimmten Stelle. Im Hochpunkt haben wir eine negative Krümmung, dass heißt eine Linkskurve des Graphenverlaufs. Entsprechend haben wir im Tiefpunkt eine positive Krümmung, also eine Rechtskurve des Graphenverlaufs. Es gilt:
\( \quad \begin{array}{ l*{4}{l} } Hochpunkt : & f''(x) & < & 0 \\[6pt] Tiefpunkt : & f''(x) & > & 0 \\ \end{array} \)
\(\\\)
Wir sehen in der Skizze, dass sowohl im Wendepunkt als auch im Sattelpunkt ein Wechsel des Krümungsverhaltens vorliegt, hier jeweils ein Wechsel von einer Rechtskurve in eine Linkskurve, wenn man sich den Graphen als eine Bahn, auf der man sich bewegt, vorstellt. Es kann natürlich auch ein Wechsel von einer Linkskurve in eine Rechtskurve vorliegen.
\(\\\)
Für die Stammfunktion \(H\) von der Funktion \(h\)
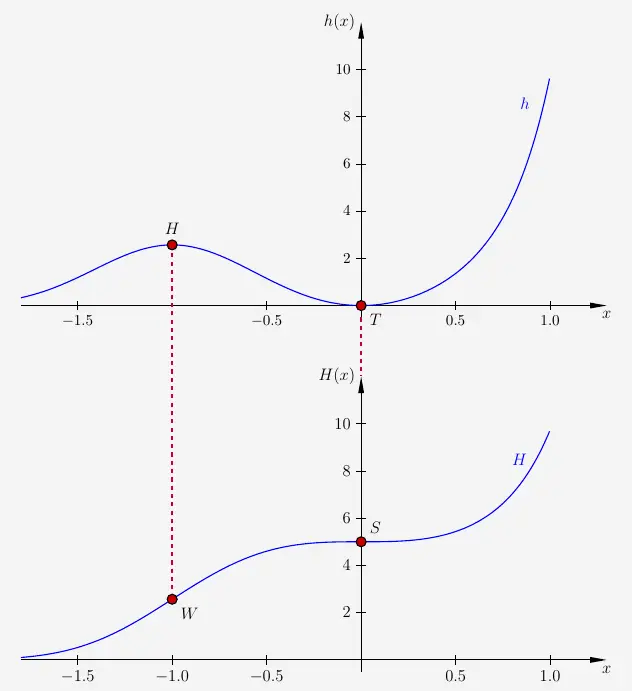
gilt, dass sie bei dem \(x\)-Wert einen Wendepunkt hat, wo bei \(h\) ein Extrempunkt ist und dass sie bei dem \(x\)-Wert einen Sattelpunkt hat, wo bei \(h\) sowohl ein Extrempunkt als auch eine Nullstelle ist. Das heißt, die Stammfunktionen von \(h\) haben bei ca. \(x=-1\) einen Wendepunkt und bei \(x=0\) einen Sattelpunkt.
Daraus folgt, dass sich das Krümmungsverhalten der Stammfunktionen 2-mal ändert im Bereich von \(-1.5\leq x \leq1\), was im Widerspruch zu der Aussage steht.
\(\\[2em]\)
Aufgabe 2 – Graphen
Die Funktion \(H\) mit
\( \quad H(x) = \displaystyle{\int}_0^x h(t) dt \)
\(\\\)
drückt eine Stammfunktion der Funktion \(h\) aus, die in der vorherigen Aufgabe untersucht wurde.
Welcher Graph hat nun die festgestellten Eigenschaften?
Graph III besitzt einen Wendepunkt und einen Sattelpunkt. Allerdings liegt der Wendepunkt bei \(x=0\) und der Sattelpunkt bei einem \(x>0\). Damit kommt Graph III nicht infrage.
Graph II hat zwar einen Wendepunkt, der ebenfalls eine Nullstelle ist, bei einem \(x<0\). Das würde passen. Aber leider liegt bei \(x=0\) ein Tiefpunkt, was bei der Stammfunktion \(H\) von der gegebenen Funktion \(h\) nicht sein soll.
Allein Graph I erfüllt die Voraussetzungen mit einem Sattelpunkt bei \(x=0\) und einem Extrempunkt bei \(x<0\).
\(\\\)