Funktion h
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – positive Funktionswerte
Wir betrachten bei
\( \quad h(x) = 5x^2 \cdot e^{\frac{2}{3}x^3} \)
\(\\\)
die Terme
\( \quad 5x^2 \quad \textrm{und} \quad e^{\frac{2}{3}x^3} . \)
\(\\\)
Der Graph von \(5x^2\) stellt eine nach oben geöffnete Parabel mit dem Scheitelpunkt im Koordinatenursprung wie dargestellt.
\(\\\)
Graphen von e-Funktionen in der Form
\( \quad a \cdot e^{k(x)} \quad \textrm{mit} \quad a \in \mathbb{R} \; , \; x \in \mathbb{R} \; , \; k(x) \; \textrm{ist ganzrational} \)
\(\\\)
haben bestimmte Verläufe.
Verlaufsformen bei einem positiven \(a\)-Wert:
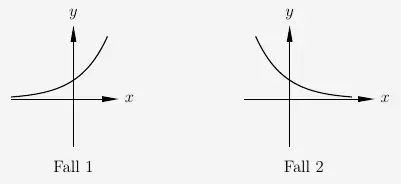
\(\\\)
Verlaufsformen bei einem negativen \(a\)-Wert:
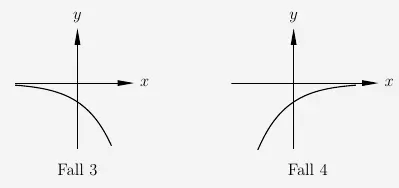
\(\\\)
Für \(e^{\frac{2}{3}x^3}\) sind die Funktionswerte also stets positiv. Damit haben sowohl \(e^{\frac{2}{3}x^3}\) als auch \(5x^2\) nie negative Funktionswerte. Folglich gibt es auch bei
\( \quad h(x) = 5x^2 \cdot e^{\frac{2}{3}x^3} \)
\(\\\)
keine negativen Funktionswerte.
\(\\[2em]\)
Aufgabe 2 – erste Ableitung
\( \quad h(x) = 5x^2 \cdot e^{\frac{2}{3}x^3} = u(x) \cdot v(x) \)
\(\\\)
wird mit der Produktregel
\( \quad h'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x) \)
\(\\\)
oder in der Kurzschreibweise
\( \quad h'(x) = u' \cdot v + u \cdot v' \)
\(\\\)
abgeleitet. Dabei ist
\( \quad \begin{array}{ r c l c r c l c l } u(x) & = & 5x^2 & & & & & & \\[6pt] u'(x) & = & 10x & & & & & & \\[6pt] v(x) & = & e^{\frac{2}{3}x^3} & = & r \big( s(x) \big) & & & & \\[24pt] & & & & s(x) & = & \frac{2}{3}x^3 & \Leftrightarrow & innerer \; Ausdruck \\[6pt] & & & & s'(x) & = & 2x^2 & \Leftrightarrow & innere \; Ableitung \\[6pt] & & & & r(s) & = & e^s & \Leftrightarrow & \ddot{a}ußerer \; Ausdruck \\[6pt] & & & & r'(s) & = & e^s & \\[6pt] & & & & r' \big( s(x) \big) & = & e^{\frac{2}{3}x^3} & \Leftrightarrow & \ddot{a}ußere \; Ableitung \\[6pt] \end{array} \)
\(\\\)
\( \quad \begin{array}{ r c l l l } v'(x) & = & s'(x) \cdot r' \big( s(x) \big) & \Leftrightarrow & innere \; Ableitung \times \ddot{a}ußere \; Ableitung \\[6pt] v'(x) & = & 2x^2 \cdot e^{\frac{2}{3}x^3} & & \\ \end{array} \)
\(\\\)
Weiter mit der Produktregel :
\( \quad \begin{array}{ r c l l } h'(x) & = & 10x \cdot e^{\frac{2}{3}x^3} + 5x^2 \cdot 2x^2 \cdot e^{\frac{2}{3}x^3} & \qquad \rightarrow e^{\frac{2}{3}x^3} \; ausklammern \\[6pt] & = & \left( 10x + 10x^4 \right) \cdot e^{\frac{2}{3}x^3} & \qquad \rightarrow 10x \; ausklammern \\[6pt] & = & 10x \cdot \left( 1 + x^3 \right) \cdot e^{\frac{2}{3}x^3} & \\ \end{array} \)
\(\\[2em]\)
Aufgabe 3 – waagerechte Tangenten
Bei waagerechten Tangenten an den Graphen gilt
\( \quad \begin{array}{ r c l } h'(x) & = & 0 \\[6pt] 0 & = &10x \cdot \left( 1 + x^3 \right) \cdot e^{\frac{2}{3}x^3} \\ \end{array} \)
\(\\\)
Da \(e^{\frac{2}{3}x^3}\not=0\) ist, gehen wir mit der Regel vom Nullprodukt
,,Ist \(a \cdot b = 0\), so ist \(a=0\) und/oder \(b=0\).‘’
\(\\\)
von
\( \quad 10x=0 \quad \textrm{und} \quad 1 + x^3 = 0 \)
aus.
\( \quad \begin{array}{ r c l l } 10x & = & 0 & | \; : 10 \\[6pt] x_1 & = & 0 & \\[24pt] 1 + x^3 & = & 0 & | -1 \\[6pt] x^3 & = & -1 & \Bigl| \sqrt[3]{\dots} \\[6pt] x_2 & = & -1 & \\ \end{array} \)
\(\\\)
Ausgehend von der allgemeinen Geradengleichung
\( \quad y = mx + b \)
\(\\\)
können wir die Tangentengleichung bei einer waagerechten Tangente, also \(m=0\) vereinfachen zu \(y = b\) .
Wir bestimmen \(b\) , indem wir die \(y\)-Werte unserer Lösungen ermitteln:
\( \quad \begin{array}{ r c l } h(0) & = & 5 \cdot 0^2 \cdot e^{\frac{2}{3} \cdot 0^3} \\[6pt] h(0) & = & 0 \\[24pt] h(-1) & = & 5 \cdot (-1)^2 \cdot e^{\frac{2}{3} \cdot (-1)^3} \\[6pt] h(-1) & = & 5 \cdot e^{-\frac{2}{3}} \\ \end{array} \)
\(\\\)
Damit erhalten wir \(b_1=0\) und \(b_2=5 \cdot e^{-\frac{2}{3}}\) . Das heißt, dass wir die Tangentengleichungen
\( \quad \begin{array}{ r c l } y_1 & = & 0 \\[6pt] y_2 & = & 5 \cdot e^{-\frac{2}{3}} \\ \end{array} \)
\(\\\)
erhalten. \(y_1\) ist die \(x\)-Achse und \(y_2\) die angegebene Gerade \(t\) .
\(\\[2em]\)
Aufgabe 4 – Fläche zwischen t und h
Um die Fläche zwischen \(g\) und \(t\) zu berechnen,
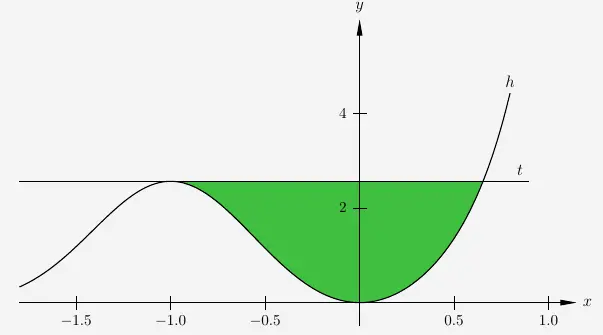
\(\\\)
brauchen wir den 2.Schnittpunkt. Dazu setzen wir die Funktionsgleichungen gleich:
\( \quad \begin{array}{ r c l l } t(x) & = & g(x) & | -t(x) \\[6pt] 0 & = & g(x) - t(x) & \\[6pt] 0 & = & 5 \cdot x^2 \cdot e^{\frac{2}{3} \cdot x^3} -5 \cdot e^{-\frac{2}{3}} & \\ \end{array} \)
\(\\\)
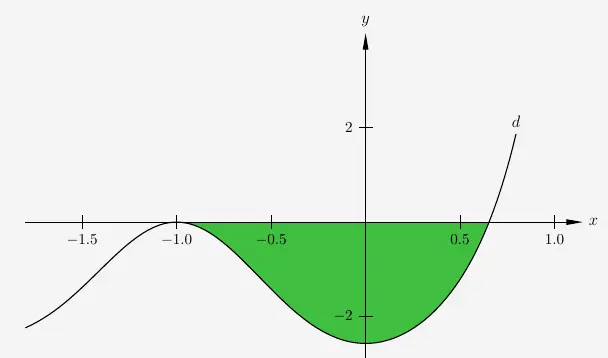
Den rechten Teil der Gleichung nennen wir die Differenzfunktion \(d\) mit
\( \quad d(x) \; = \; 5 \cdot x^2 \cdot e^{\frac{2}{3} \cdot x^3} -5 \cdot e^{-\frac{2}{3}} \; , \)
\(\\\)
wobei \(d(x) = 0\) ist.
\(\\\)
Mit den herkömmlichen Lösungsverfahren wie
können wir die Nullstellen von \(d\) nicht berechnen. Wir müssen auf ein Näherungsverfahren wie zum Beispiel das Newton-Verfahren zurückgreifen. Alternativ dazu kann man aber auch bei den höheren Taschenrechnerfunktionen den Solve-Befehl verwenden, der ja auch auf einen Näherungsalgorithmus basiert.
Mit dem Casio fx 991-DE X schreiben wir

mit dem \(\color{#CC0000}{roten}\) Gleichheitszeichen. Die Tastenkombination \(\boxed{\color{#C19A6B}{SHIFT}}\) \(\boxed{CALC}\) liefert

Wie die obige Zeichnung zeigt, muss die gesucht Nullstelle zwischen \(0{,}5\) und \(1\) liegen. Wir geben für die Berechnung den Startwert \(0{,}5\) vor.

Wir bestätigen zweimal mit \(\boxed{=}\).

Die gesuchte Nullstelle liegt bei \(x=0{,}653\).
\(\\\)
Die von \(t\) und \(h\) eingeschlossene Fläche wird berechnet mit
\( \begin{array}{ r c l } A & = & \Biggl|\displaystyle{\int}_{-1}^{0.653} d(x) dx \Biggl| \\[8pt] & = & \Biggl| \displaystyle{\int}_{-1}^{0{,}653} \left( 5 \cdot x^2 \cdot e^{\frac{2}{3} \cdot x^3} -5 \cdot e^{-\frac{2}{3}} \right) \, dx \Biggl| \\[8pt] & = & \bigl|-2{,}517 \bigl| \\[8pt] & = & 2{,}517 \\ \end{array} \)
\(\\\)