Aufgaben

---

\(\\\)

“Digitales Messgerät”

Ein digitales Messgerät misst bei einem Diabetes-Patienten kontinuierlich den Glukosewert (Blutzuckerwert). Der Glukosewert dieses Patienten wird in Abhängigkeit von der Zeit \(t\) im Intervall \([0 ; 3{,}75]\) mit Hilfe der Funktion \(g\) mit

\( \quad g(t) \; = \; 13 \cdot t^3 - 78 \cdot t^2 + 104 \cdot t + 96 \)

modelliert. Dabei wird der Glukosewert \(g(t)\) in \(u\) (Units) und die Zeit \(t\) in \(h\) (Stunden) seit Messbeginn angegeben. Die Abbildung 1

\(\quad\)

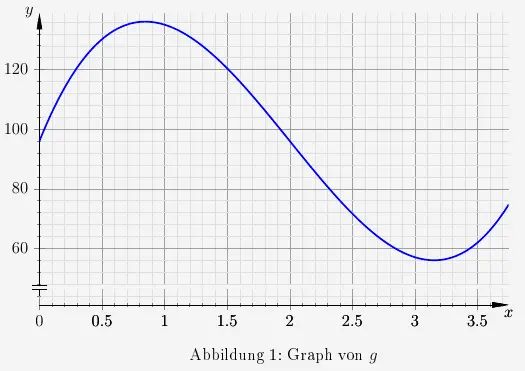
zeigt den Graphen von \(g\) im betrachteten Intervall.

\(\\[1em]\)

Unterzuckerung

1. Bei einem Glukosewert von unter \(70 \; u\) spricht man von Unterzuckerung. Bestimmen Sie mit Hilfe des Graphen die Länge des Zeitraums, in dem Unterzuckerung vorliegt.

   (2 P)

\(\\\)

2. Etwas mehr als 3 Stunden nach Messbeginn liegt im Bereich der Unterzuckerung der niedrigste Glukosewert. Berechnen Sie den zugehörigen Zeitpunkt.

   (3 P)

\(\\\)

3. Weisen Sie nach, dass der Glukosewert eine Stunde nach Messbeginn um mehr als \(40\%\) größer ist als zu Beginn der Messung.

   (3 P)

\(\\\)

4. Berechnen Sie den durchschnittlichen Glukosewert innerhalb der ersten 2 Stunden nach Messbeginn.

   (3 P)

Lösung

\(\\[1em]\)

Änderungsraten

Aus medizinischer Sicht ist ein zu schnelles Absinken des Glukosewerts gefährlich.

\(\\\)

1. \(T(2|-52)\) ist der tiefste Punkt des Graphen der Ableitungsfunktion \(g'\) über dem Intervall \([0 ; 3{,}75]\).
   Interpretieren Sie dies im Sachzusammenhang.

   (3 P)

\(\\\)

2. Die folgenden Terme beschreiben unterschiedliche Änderungsraten der Funktion \(g\).
   \(\\\) \(\qquad\)
   • Term A: \(\quad \frac{g(3) - g(1)}{3 - 1}\)
     \(\\\) \(\qquad\)
   • Term B: \(\quad \lim \limits_{h \to 0} \frac{g(1 + h) - g(1)}{h}\)

Geben Sie an, welche Änderungsraten diese beiden Terme beschreiben.

(4 P)

\(\\\)

3. Liegt die momentane Änderungsrate unter einem Wert von \(-40\frac{u}{h}\), so zeigt das Messgerät des Patienten ein Warnsymbol an.
   Weisen Sie nach, dass dieses Warnsymbol im betrachteten Zeitintervall mehr als eine Stunde angezeigt wird.

   (4 P)

Lösung

\(\\[1em]\)

Funktionenschar f

Gegeben ist die Funktionenschar \(f_a\) mit

\(\quad f_a(t) \; = \; a \cdot \left(t^3 - 4 \cdot t \right) \quad \text{und}\; a > 0\)

Auf dem Beiblatt zeigt die Abbildung 2 den Graphen von \(f_1\).

\(\quad\)

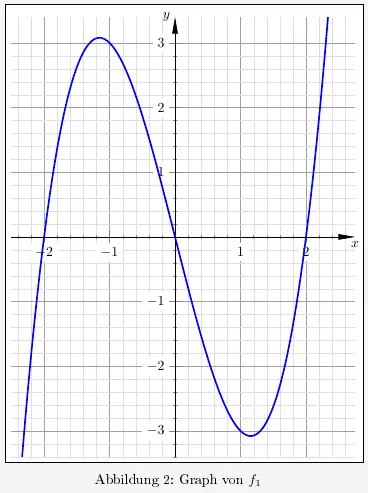
\(\qquad \qquad\) Beiblatt ausdrucken

\(\\\)

1. Für jedes \(a > 0\) hat der Graph von \(f_a\) genau einen Hochpunkt \(H_a\).
   Beschreiben Sie, wie sich die Lage von \(H_a\) ändert, wenn sich der Wert des Parameters \(a\) verdreifacht.

   (3 P)

\(\\\)

2. Die Tangente an den Graphen von \(f_a\) im Punkt \((2|0)\) schließt mit der \(t\)-Achse einen Winkel ein.
   Bestimmen Sie denjenigen Wert für \(a\), für den dieser Winkel \(45^\circ\) beträgt.

   (3 P)

\(\\\)

3. Weisen Sie durch Rechnung nach:
   Verschiebt man den Graphen von \(g\) nach links entlang der \(t\)-Achse um \(2\) Einheiten und anschließend entlang der \(y\)-Achse nach unten um \(96\) Einheiten, so erhält man einen Graphen, der zur Schar \(f_a\) gehört.

   (5 P)

Lösung

\(\\[1em]\)

Funktionenschar h

Gegeben ist die Funktionenschar \(h_a\) mit

\(\quad h_a(t) \; = \; -a \cdot t \quad \text{und} \; a > 0\)

\(\\\)

Betrachtet wird der folgende Term:

\( \quad \begin{array}{ r c l } \begin{vmatrix} \displaystyle{\int}_1^{t_0} f_a(t) dt \end{vmatrix} & - & \begin{vmatrix} \displaystyle{\int}_1^{t_0} h_a(t) dt \end{vmatrix} \\ \end{array} \)

\(\\\)

Dabei ist \(t_0\) diejenige Lösung der Gleichung \(f_a(t) = h_a(t)\), für die \(1 < t_0 < 2\) gilt.

\(\\[1em]\)

1. Zeichnen Sie in Abbildung 2 ein Flächenstück ein, dessen Inhalt mit dem angegebenen Term für \(a=1\) berechnet werden kann.

   (2 P)

\(\\\)

2. Berechnen Sie \(t_0\) sowie den Wert des obigen Terms in Abhängigkeit von \(a\).

   (5 P)

Lösung

\(\\[2em]\)