Binomialverteilung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Treffer bei 20 Schüssen
genau 14
Wir berechnen die Binomialverteilung mit der Bernoullikette
\( \quad P(x = k) = \displaystyle{\binom{n}{k}} \cdot p^k \cdot (1-p)^{n-k} \)
\(\\\)
Wir benötigen also \(n\), \(p\) und \(k\) und wählen
\( \quad \begin{array}{ r c c } n & = & 20 \\[6pt] p & = & 0{,}7 \\[6pt] k & = & 14 \\ \end{array} \)
\(\\\)

\(\\\)
Mit \(P_{n;p}(x=k)\) ist also \(P_{20;0{,}7}(x = 14)\) zu berechnen.
Möglich ist die Berechnung auf dreierlei Arten:
- mit der Bernoullikette
- mit den Tabellenwerken
- mit der Taschenrechnerfunktion für Verteilungen
\(\\[2em]\)
Bernoullikette
Wir setzen \(n=20\), \(p=0{,}7\) und \(k=14\) in die Bernoulliformel ein.
\( \quad P(x = 14) = \displaystyle{\binom{20}{14}} \cdot 0{,}7^k \cdot (1-0{,}7)^{20-14} \; = \; 0{,}1916 \)
\(\\[2em]\)
Tabelle für Einzelwerte
Bei Einzelwerten verwenden wir \(B_{n;p}(k)\) oder auch \(B(n;p;k)\) mit \(n=20\), \(p=0{,}7\) und \(k=14\) .
Wir wählen die Tabelle mit \(n=20\) .

Da \(p=0{,}7>0{,}5\) ist, lesen wir von unten und rechts (grau unterlegt) die Wahrscheinlichkeit
\( \quad P(x = 14) \; = \; 0{,}1916 \)
\(\\\) ab.
\(\\[2em]\)
Taschenrechnerfunktion für Einzelwerte
Wer einen Taschenrechner mit den Funktionen für Verteilungen hat oder aber über den Bereich dist für distribution verfügt, kann auf einfache Weise den Wert berechnen.
Mit beispielsweise dem CASIO fx-991DE X CLASSWIZ gehen wir auf \(\boxed{MENU}\) und mit den Pfeiltasten nach rechts bis

erscheint. Wir bestätigen mit \(\boxed{=}\).
\(\\\)

Wir wählen die Binomial-Dichte mit \(\boxed{4}\)
\(\\\)

und danach die \(\boxed{2}\).
\(\\\)

Wir geben die Werte ein,
\(\\\)

wobei wir jede Eingabe mit \(\boxed{=}\) bestätigen. Das Ergebnis erhalten wir mit noch einmal \(\boxed{=}\).
\(\\\)

\(\\[2em]\)
mindestens 10
In diesem Fall ist die Anzahl der Treffer \(k \geq 10\), als Histogramm also

\(\\\)
Wir berechnen den Bereich von 10 bis 20 über das Gegenereignis mit
\( \quad P(x \geq 10) \; = \; 1 - P(x \leq 9) \)
\(\\\)
und können dies auf zweierlei Arten machen:
- mit den Tabellenwerken
- mit der Taschenrechnerfunktion für Verteilungen
\(\\[2em]\)
Tabelle für kumulierte Wahrscheinlichkeiten
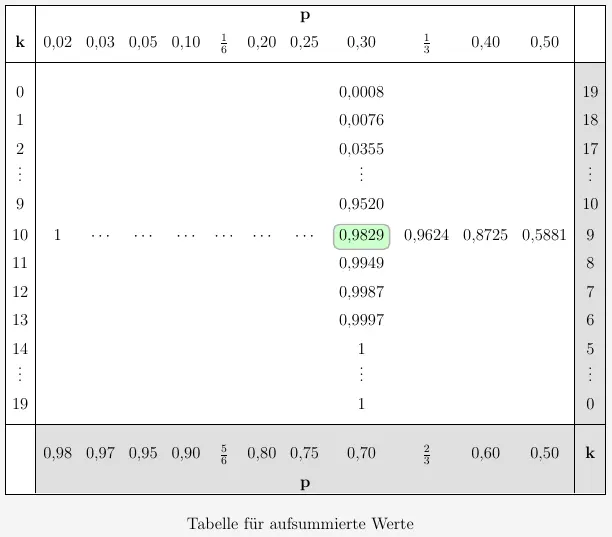
Bei Bereichen verwenden wir \(F_{n;p}(k)\) oder auch \(F(n;p;k)\) mit \(n=20\), \(p=0{,}7\) und \(k=9\).
Wir wählen die Tabelle mit \(n=20\).
\(\\\)
Da \(p=0{,}7>0{,}5\) ist, lesen wir von unten und rechts (grau unterlegt) die Wahrscheinlichkeit \(p=0{,}9829\) ab. Der so abgelesene Wert (von unten und rechts) muss bei den Summenverteilungen von \(1\) abgezogen werden. Es ergibt sich
\( \quad P(x \leq 9) \; = \; 1 - 0{,}9829 \)
\(\\\)
Die Wahrscheinlichkeit für \(x \geq 10\) ist also
\( \quad \begin{array}{ r c l } P(x \geq 10) & = & 1 - P(x \leq 9) \\[6pt] & = & 1 - (1 - 0{,}9829) \\[6pt] & = & 1 - 1 + 0{,}9829 \\[6pt] & = & 0{,}9829 \\[6pt] & = & 98{,}29 \% \\ \end{array} \)
\(\\[2em]\)
Taschenrechnerfunktion für kumulierte Wahrscheinlichkeiten
Für \(P(x \leq 9)\) nutzen wir die kumulierte Binomialverteilung des CASIO fx-991DE X CLASSWIZ und gehen auf \(\boxed{MENU}\) \(\boxed{7}\) und mit den Pfeiltasten nach unten.

Wir wählen \(\boxed{1}\)
\(\\\)

und dann \(\boxed{2}\).
\(\\\)

Wir geben die Werte ein und bestätigen jeweils mit \(\boxed{=}\).
\(\\\)

Anschließend noch einmal \(\boxed{=}\) .
\(\\\)

\(\\\)
Wir berechnen die gesuchte Wahrscheinlichkeit mit
\( \quad \begin{array}{ r c l } P(x \geq 10) & = & 1 - P(x \leq 9) \\[6pt] & = & 1 - 0{,}0171 \\[6pt] & = & 0{,}9829 \\[6pt] & = & 98{,}29 \% \\ \end{array} \)
\(\\[2em]\)
mehr als 60% und weniger als 80%
Zunächst müssen wir feststellen, was 60% und 80% der Schüsse sind, was wir mit \(n \cdot p\) ermitteln.
\( \quad \begin{array}{ r c l } 20 \cdot 0{,}6 & = & 12 \\[6pt] 20 \cdot 0{,}8 & = & 16 \\ \end{array} \)
\(\\\)
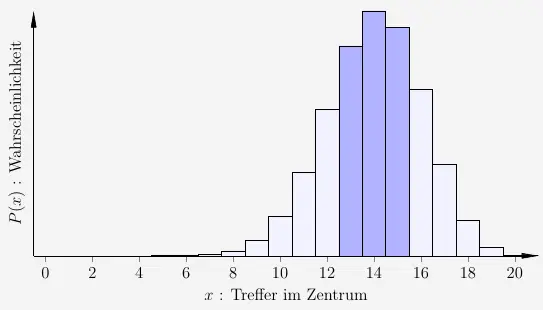
Mit \(12<k<16\) handelt es sich lediglich um die \(x\)-Werte \(13\), \(14\) und \(15\).
\(\\\)
Die Wahrscheinlichkeiten können bei nur 3 Werten einzeln berechnet und dann aufaddiert werden oder aber über die kumulierten Wahrscheinlichkeiten berechnet werden. Ich wähle hier den zweiten Weg. Es ist
\( \quad \begin{array}{ r c c c l } P(x=k) & = & P(12 < x < 16) & = & P(x \leq 15) - P(x \leq 12) \\ \end{array} \)
\(\\\)
Hier haben wir wieder zwei Optionen:
- mit den Tabellenwerken
- mit der Taschenrechnerfunktion für Verteilungen
\(\\[2em]\)
Bereich mit der Tabelle ermitteln
Bei Bereichen verwenden wir \(F_{n;p}(k)\) oder auch \(F(n;p;k)\) mit \(n=20\) und \(p=0{,}7\) .

\(\\\)
Damit ist
\( \quad \begin{array}{ r c c c l } P(12 < x < 16) & = & (1-0{,}2375) - (1-0{,}7723) & = & 0{,}5348 \\ \end{array} \)
\(\\[2em]\)
Taschenrechnerfunktion bei Bereichen
Mit dem CASIO fx-991DE X CLASSWIZ können wir mit einer Liste arbeiten. Wir gehen auf \(\boxed{MENU}\) \(\boxed{7}\) und mit den Pfeiltasten nach unten.

Wir wählen \(\boxed{1}\)
\(\\\)

und noch einmal die \(\boxed{1}\).
\(\\\)

Wir geben die Werte ein und bestätigen jeweils mit \(\boxed{=}\).
\(\\\)

Anschließend noch einmal \(\boxed{=}\) drücken.
\(\\\)

Wir bestätigen die Eingaben jeweils mit \(\boxed{=}\) und drücken wieder \(\boxed{=}\) .
\(\\\)

\(\\\)
Damit ist
\(\quad \begin{array}{ r c c c l } P(12 < x < 16) & = & 0{,}7624 - 0{,}2277 & = & 0{,}5347 \\ \end{array} \)
\(\\[2em]\)
Aufgabe 2 – Mindestanzahl an Schüssen
Die Trefferwahrscheinlichkeit ist auch hier \(p=0{,}7\). Wie verhält sich nun die Wahrscheinlichkeit bei steigender Anzahl an Schüssen? Dazu 2 Beispiele:
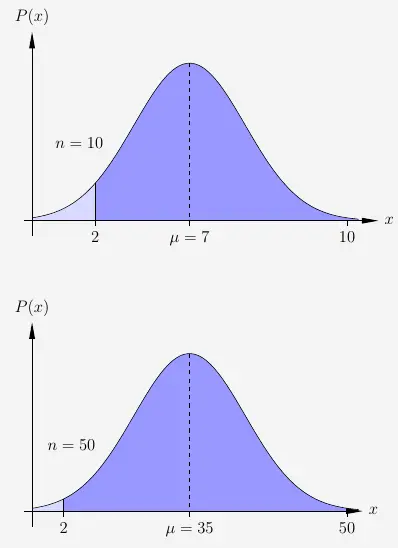
Es ist zu erkennen, dass bei steigender Anzahl an Schüssen die rechte Fläche prozentual im weiter anwächst. Denn bei größer werdenden \(n\) verschiebt sich die Kurve immer weiter nach rechts, so dass die Fläche links von \(x=2\) prozentual immer kleiner wird.
Es gilt Folgendes:
\( \quad \begin{array}{ r c r l } P(x \geq 2) & > & 0{,}99 \\[6pt] 1 - P(x \leq 1) & > & 0{,}99 & | - 1 \\[6pt] -P(x \leq 1) & > & -0{,}01 & | \cdot (-1) \\[6pt] P(x \leq 1) & < & 0{,}01 \\[6pt] \end{array} \)
\(\\\)
Wir formen \(P(x \leq 1)\) in einen Term um.
\( \quad \begin{array}{ r c l } P(x \leq 1) & = & P(x = 0) + P(x = 1) \\[6pt] P(x \leq 1) & = & \displaystyle{\binom{n}{0}} \cdot 0{,}7^0 \cdot 0{,}3^{n} +\displaystyle{\binom{n}{1}} \cdot 0{,}7^1 \cdot 0{,}3^{n-1} \\ \end{array} \)
\(\\\)
Da nun \(\displaystyle{\binom{n}{0}}=1\), \(\displaystyle{\binom{n}{1}}=n\) und \(0{,}7^0=1\) ist, erhalten wir die vereinfachte Gleichung
\( \quad \begin{array}{ r c l } P(x \leq 1) & = & 0{,}3^{n} + n \cdot 0{,}7 \cdot 0{,}3^{n-1} \\ \end{array} \)
\(\\\)
Mit der Tabellenfunktion des Taschenrechners lassen sich nun schnell die Wahrscheinlichkeiten von \(P(x \leq 1)\) aufsteigend anzeigen bei \(n=2\) beginnend. Mit dem CASIO fx-991DE X CLASSWIZ wählen wir zum Beispiel den Bereich von \(2\) bis \(10\) . Dazu wählen wir \(\boxed{MENU}\) \(\boxed{9}\) und geben den Term mit \(x\) statt \(n\) ein.

Wir bestätigen zweimal mit \(\boxed{=}\).
\(\\\)

Es erscheinen folgende Werte:

\(\\\)
Mit \(n=7\) ist
\(\quad P(x \geq 2) \; = \; 1 - 0{,}0038 \; = \; 0{,}9962 \; = \; 99{,}62\% \)
\(\\\)
Nike muss mindestens \(7\) Schüsse abgeben, um mit einer Wahrscheinlichkeit von mehr als \(99\%\) mindestens zweimal ins Zentrum zu treffen.
\(\\\)