HMF 2 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Integral
Es gilt
\(\quad \displaystyle{\int}_1^7 f(x) dx \; = \; F(7) - F(1) \)

Es ist zu erkennen, dass bei dem Graphen \(G_F\)
\(\quad \begin{array}{ r c l } F(1) & = & 1 \\[6pt] F(7) & = & 5 \\ \end{array} \)
\(\\\)
ist. Es folgt
\(\quad \displaystyle{\int}_1^7 f(x) dx \; = \; 5 - 1 \; = \; 4 \)
\(\\[2em]\)
Aufgabe 2 – Funktionswert an der Stelle 1
Der Funktionswert von \(f\) wird mit der Steigung der Stammfunktion \(F\) bestimmt. Wir legen dazu eine Tangente bei \(x=1\) an den Graphen und lesen die Steigung am Steigungsdreieck ab.
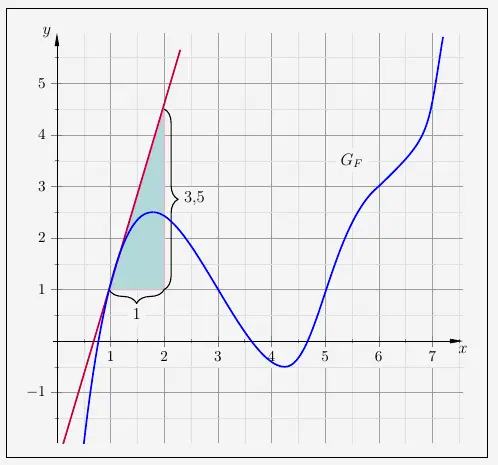
\(\quad f(1) = \frac{3{,}5}{1} = 3{,}5 \)
\(\\\)