Sturzflug
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Parameter a und b
Wir definieren \(s\). Dabei ist zu beachten, dass sie die Variable \(a\) enthält, die wir ja schon als die Funktion \(a(r)\) verwendet haben. Diese Definition muss zunächst gelöscht werden. Alternativ kann man natürlich auch eine Variable wählen, die noch nicht verwendet wurde.
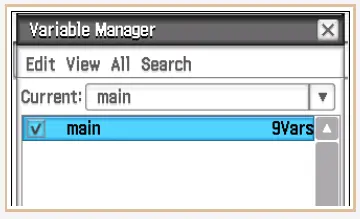
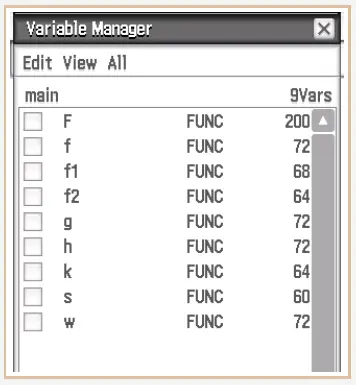
Dazu gehen wir oben links in den Variablenmanager:

\(\\\)
Wir wählen main aus und öffnen dies mit einem Doppelklick.
\(\\\)
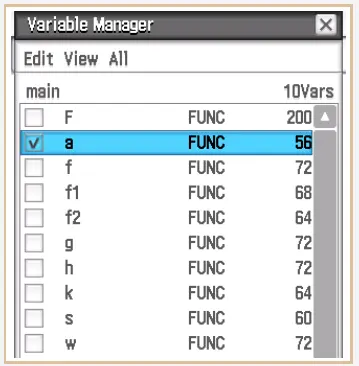
Bis auf \(a\) nehmen wir alle Haken weg undmarkieren die Zeile mit \(a\) .
\(\\\)
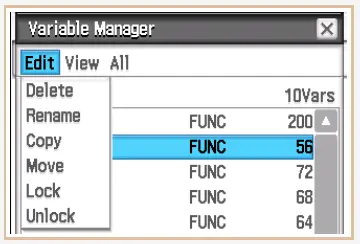
Wir wählen Edit und Delete.
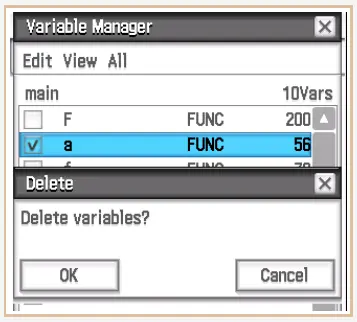
und bestätigen mit OK.
\(a\) ist nun entfernt. Wir können den Variablenmanager schließen.
\(\\\)
Jetzt definieren wir \(s\) .
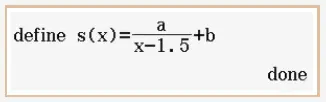
\(\\\)
Die Funktion \(s\) hat bei \(x=0,5\) den gleichen Funktionswert wie die Funktion \(k\), denn dort geht die eine Funktion in die andere über. Außerdem ist die Flugkurve in jedem Punkt knickfrei, also auch dort. Das heisst
\( \quad \begin{align} \text{I} && s(0.5) & = k(0.5) \\[6pt] \text{II} && s'(0.5) & = k'(0.5) \end{align} \)
\(\\\)
Wir lösen das lineare Gleichungssystem indem wir dieses Werkzeug benutzen:

\(\\[2em]\)
Aufgabe 2 – Steigungswinkel

Wie hier im Steigungsdreieck zu sehen ist gelten die Verhältnisse
\( \quad m=\tfrac{\Delta y}{\Delta x} = \tfrac{Gegenkathete}{Ankathete} = tan(\alpha) \)
\(\\\)
Daraus ergibt sich
\( \quad m=tan(85^\circ) \)
\(\\\)
Weiter gilt
\( \quad m=s'_{-0.75,1.6875}(x) \)
\(\\\)
Folglich berechnen wir die horizontale Entfernung \(x=e\) mit dem Ansatz
\( \quad s'_{-0.75,1.6875}(x)=tan(85^\circ) \)
\(\\\)
Wir definieren \(r\) mit den Werten von \(a\) und \(b\) eingesetzt in die Funktion \(s\)

\(\\\)
und berechnen die Gleichung.
Achtung: Die Winkeleinstellung muss auf 360° eingestellt sein.

\(\\\)
Wenn wir uns den Graphen von \(r\) betrachten, sehen wir, dass \(r\) einen typischen Verlauf einer gebrochen-rationalen Funktion und bei \(x=1{,}5\) eine Definitionslücke hat.

\(\\\)
Wir überprüfen die beiden Ergebnissen.

\(\\\)
Der 2. \(y\)-Wert ist negativ, was nicht sein kann. Also ist der richtige Wert \(x=1{,}2438\) .
\(\\[2em]\)
Aufgabe 3 – Länge der Flugkurve S
Die Funktion \(h\) kann für die Flugkurve \(S\) beschrieben werden mit
\( \quad h(x)=\left\{ \begin{array}{ c l } k(x) & \textit{mit} \quad 0 \leq x \leq 0{,}5 \\[6pt] r(x) & \textit{mit} \quad 0{,}5 < x \leq 1{,}2438 \\ \end{array} \right. \)
\(\\\)
Wir erhalten die Länge von \(S\) mit

\(\\\)
Die Länge \(L\) der Kurve \(S\) beträgt 3,033 m.
\(\\\)