Alternativtest

Inhaltsverzeichnis

\(\\\)

Bei einem Hypothesentest werden grundsätzlich zwei Hypothesen einander gegenüber gestellt. Anhand des Testergebnisses entscheidet man sich für eine der beiden Hypothesen.

\(\\[1em]\)

Annahme- und Verwerfungsbereich

Starten wir mit einem Beispiel:

Timo hat zwei äußerlich nicht voneinander unterscheidbare Würfel. Der eine ist ein gewöhnlicher LaPlace-Würfel (alle Zahlen auf dem Würfel haben die gleiche Trefferwahrscheinlichkeit). Von dem anderen Würfel weiß er, dass durchschnittlich jeder dritte Wurf eine \(6\) zur Folge hat.

Timo weiß jetzt nicht mehr, welcher von den beiden der gezinkte Würfel ist. Deshalb startet er eine Versuchsreihe mit \(60\) Würfen, wobei er die Anzahl der gefallenen Sechsen zählt.

Gehen wir nun davon aus, dass der eine Würfel die Wahrscheinlichkeit von \(p=\frac{1}{6}\) und der andere Würfel die Wahrscheinlichkeit \(p=\frac{1}{3}\) hat. Daraus ergeben sich die Hypothesen

\( \quad \begin{array}{ r l } h_1: & p = \frac{1}{6} \\ h_2: & p = \frac{1}{3} \\ \end{array} \)

\(\\\)

Die Wahrscheinlichkeitsverteilungen stellen sich als Histogramm folgendermaßen dar:

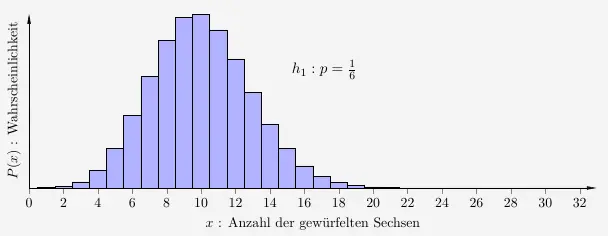
my image

my image

\(\\\)

Timo weiß nun anhand der Erwartungswerte, dass bei dem LaPlace-Würfel durchschnittlich \(10\) Sechsen und beim gezinkten Würfel durchschnittlich \(20\) Sechsen fallen. Er legt nun folgende Entscheidungsregel fest:

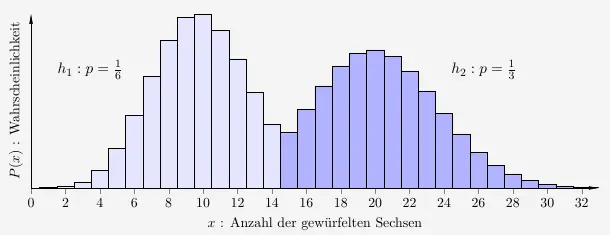
my image

\(\\\)

Fallen \(0\) bis \(14\) Sechsen, so entscheidet er sich dafür, dass es sich um den LaPlace-Würfel handelt.
Fallen \(15\) bis \(60\) Sechsen, so entscheidet er sich für den gezinkten Würfel.

Bezogen auf die Hypothese \(h_2\) heißt das linke Intervall Ablehnungs- oder Verwerfungsbereich \((V)\) und das rechte Intervall Annahmebereich \((A)\) mit

\( \quad \begin{array}{ r c l } V & = & [0 , \cdots ,14]\\ A & = & [15 , \cdots ,60]\\ \end{array} \)

\(\\\)

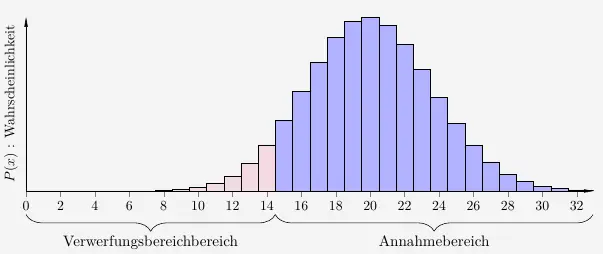
my image

\(\\[2em]\)

Fehler 1. Art und Fehler 2. Art

Die Entscheidungsregel von Timo stimmt zwar in den meisten Fällen, aber nicht immer. Denn es könnte ja durchaus sein, dass er nur \(12\) Sechsen würfelt obwohl er mit dem gezinkten Würfel würfelt. Seine Entscheidungsregel ist also mit einer gewissen Fehlerrate behaftet.

Diese Fehlerrate kann auch berechnet werden. Diese ist genau die Wahrscheinlichkeit des Verwerfungsbereichs mit

\( \quad \alpha \, = \, P_{60 \, ; \, \frac{1}{3}} (x \leq 14) \, = \, 0{,}063 \, = \, 6{,}3 \% \)

\(\\\)

Das heißt, dass das Risiko, wenn eine \(12\) gewürfelt wird, sich falsch zu entscheiden, \(6{,}3\%\) beträgt. Anders herum ausgedrückt fällt Timo eine nur zu \(93{,}7 \%\) sichere Entscheidung.

Dieser Fehler heißt der Fehler 1. Art. Bedeutungsgleiche Begriffe sind

Sei nun der Würfel tatsächlich nicht der gezinkte, sondern der LaPlace-Würfel.

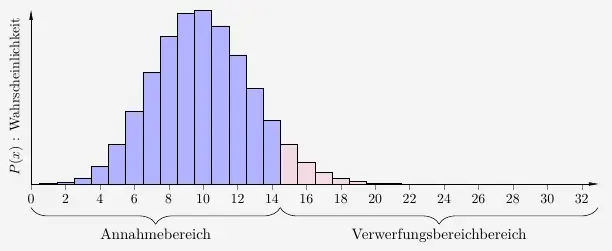
my image

Dann würde Timo bei \(20\) gewürfelten Sechsen irrtümlich bei der Entscheidung bleiben, dass dies der gezinkte Würfel ist. Diesen Fehler nennt man den Fehler 2. Art oder \(\beta\)-Fehler. Dieser wird berechnet mit

\(\\\)

\( \quad \begin{array}{ r c c c l } \beta & = & P_{60 \, ; \, \frac{1}{6}} (x > 14) & = & 1 - P_{60 \, ; \, \frac{1}{6}} (x \leq 14) \\[5pt] & & & = & 1 - 0{,}9352 \\[4pt] & & & = & 0{,}0648 \\[4pt] & & & = & 6{,}48 \% \\ \end{array} \)

\(\\[1em]\)

Fehlerarten tabellarisch

Als Tabelle noch einmal zusammen gefasst:

my image

\(\\[1em]\)

Allgemeine Formulierung der Fehlerarten

\(\\[2em]\)