Differenzierbarkeit und Stetigkeit
Inhaltsverzeichnis
\(\\\)
Differenzierbarkeit
Wann gilt eine Funktion als differenzierbar?
Eine Funktion ist differenzierbar, wenn sie an jeder Stelle eindeutig differenzierbar ist. In der Regel wird demzufolge untersucht, ob die Funktion an einer bestimmten Stelle differenzierbar ist.
Um dieses zu verdeutlichen, betrachten wir eine abschnittsweise definierte Funktion \(f\).
\(\\\)
\( \quad f(x) \, = \, \left\{ \begin{array}{ l l } x ^3 & {,} \; x \leq 1 \\[5pt] x ^2 - 4x + 4 & {,} \; x > 1 \\ \end{array}\right. \)
\(\\\)
Es ist zu erkennen, dass an der Stelle \(x=1\) die Funktion den Funktionsterm ändert. Wir untersuchen also linksseitig und rechtsseitig der \(1\) mit der ersten Ableitung die Differenzierbarkeit der Funktion.
Wir benötigen zunächst die Ableitungen der beiden Funktionsterme.
\(\\\)
\( \quad \begin{array}{ r c l c r } f(x) & = & x ^3 & {,} \; x \leq 1 \\[5pt] f'(x) & = & 3x^2 \\[10pt] f(x) & = & x ^2 - 4x + 4 & {,} \; x > 1 \\[5pt] f'(x) & = & 2x -4 \\ \end{array} \)
\(\\\)
Weiter geht’s mit der Differenzierbarkeit.
\(\\\)
\( \quad \left. \begin{array}{ r c l c r } \lim \limits_{x \uparrow 1}f'(1) & = & 3 \cdot 1^2 & = & 3 \\[6pt] \lim \limits_{x \downarrow 1}f'(1) & = & 2 \cdot 1 - 4 & = & -2 \\ \end{array} \right\} \; \Rightarrow \; \text{nicht eindeutig differenzierbar} \)
\(\\\)
Nur für den Fall, dass sowohl linksseitig als auch rechtsseitig der gleiche Wert herauskommt wäre eine Differenzierbarkeit an der Stelle \(x=1\) gewährleistet.
\(\\[1em]\)
Knickfreiheit
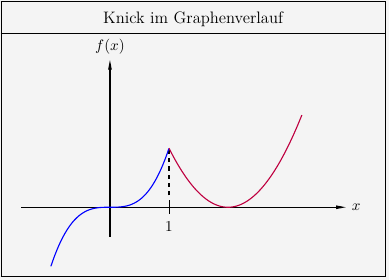
Graphisch sieht das Ganze wie folgt aus.
\(\\\)
Ist die erste Ableitung an der Stelle \(x=1\) unterschiedlich, so entsteht ein Knick. Daraus folgt, das eine differenzierbare Funktion knickfrei sein muss.
\(\\[2em]\)
Stetigkeit
Eine Funktion ist an einer Stelle \(x_0\) stetig, wenn
-
der Punkt \(P_0\left(x_0|f(x_0\right)\) definiert ist. Das heißt, dass es für \(x_0\) auch ein \(f(x_0)\) gibt.
-
es ein Intervall der Umgebung der Stelle \(x_0\) gibt. Dass heißt, dass mathematisch gesprochen, \(\lim \limits_{x \to x_0}\) existiert.
-
der Grenzwert \(\lim \limits_{x \to x_0}=f(x_0)\) existiert. Wenn also ein \(x\) in unmittelbarer Umgebung von \(x_0\) liegt, so muss auch \(f(x)\) in unmittelbarer Umgebung von \(f(x_0)\) liegen.
\(\\[1em]\)
Nicht stetige Funktionen
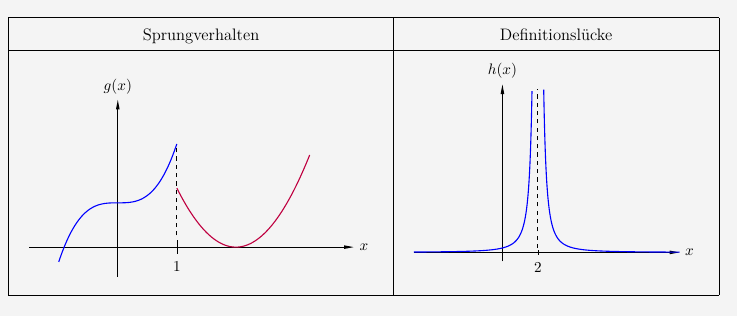
Um den Begriff der Stetigkeit besser zu verstehen ist es sinnvoll, sich nicht stetige Funktionen anzusehen. Dazu betrachten wir die folgenden 2 Fälle:
\(\\[1em]\)
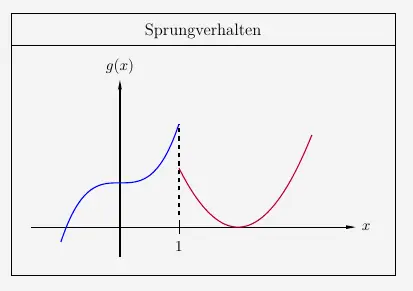
Sprungverhalten
Ein Sprung an einer Stelle,
\(\\\)
hier bei \(x=1\) bei der Funktion \(g\) mit
\(\\\)
\( \quad g(x) \, = \, \left\{ \begin{array}{ l l } x ^3 + 0{,}75 & {,} \; x \leq 1 \\[5pt] x ^2 - 4x + 4 & {,} \; x > 1 \\ \end{array}\right. \)
\(\\\)
widerspricht der dritten Voraussetzung für Stetigkeiten. Das heißt, dass es einen eindeutigen Grenzwert an der Stelle \(x_0=1\) gibt. Denn
\(\\\)
\( \quad \left. \begin{array}{ r c l c l } \lim \limits_{x \uparrow 1}g(1) & = & 1^3 + 0{,}75 & = & 1{,}75 \\[6pt] \lim \limits_{x \downarrow 1}g(1) & = & 1^2 - 4 \cdot 1 + 4 & = & 1 \\ \end{array} \right\} \; \Rightarrow \; \text{nicht eindeutig} \)
\(\\\)
hat keinen eindeutigen Grenzwert. Stetige Funktionen müssen also sprungfrei sein.
\(\\[1em]\)
Definitionslücken
Die Funktion \(j\) mit
\(\\\)
\( \quad j(x) \; = \; ln{ |x-2 | } \)
\(\\\)
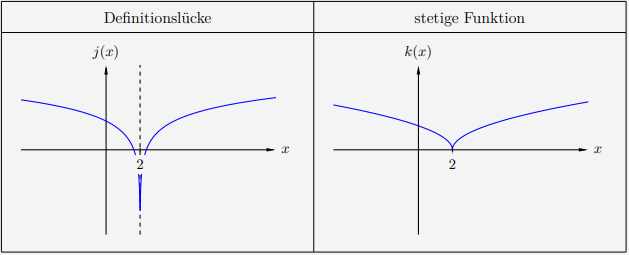
hat an der Stelle \(x=2\) eine Definitionslücke,
\(\\\)
denn \(f(2)\) führt zu dem Ausdruck \(ln(0)\), der nicht definiert ist. Denn \(ln(x)\) ist nur für \(x>0\) definiert.
Im Gegensatz dazu ist die ähnlich verlaufende Funktion \(k\) mit
\(\\\)
\( \quad k(x) \; = \; \sqrt{| x-2 |} \)
\(\\\)
stetig, denn \(k(2)=0\) und damit an der Stelle \(x=2\) definiert. \(k\) weist an dieser Stelle einen Knick auf, ist also nicht differenzierbar bei \(x=2\). Das ist aber kein Ausschlusskriterium für die Stetigkeit.
\(\\[1em]\)
Polstellen
Funktionen von der Form
\(\\\)
\( \quad f(x) \; = \; \frac{Z(x)}{N(x)} \)
\(\\\)
heißen gebrochen-rationale Funktionen. \(x\)-Werte, für die \(N(x)=0\) ist heißen Polstellen oder Pole.
\(\\\)
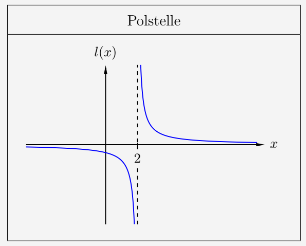
Hier ist ein Pol an der Stelle \(x=2\) dargestellt bei der Funktion \(l\) mit
\(\\\)
\( \quad l(x) \; = \; \frac{1}{x-2} \)
\(\\\)
Ein Pol ist immer eine Definitionslücke der Funktion. Außerdem ist die Polstelle stets eine Unendlichkeitsstelle. Das heißt, dass der linksseitige und rechtsseitige Grenzwert gegen \(\pm \infty\) geht. In diesem Fall ist
\(\\\)
\( \quad \begin{array}{ r c l } \lim \limits_{x \uparrow 2}l(2) & = & -\infty \\ \end{array} \)
\(\\\)
und
\(\\\)
\( \quad \begin{array}{ r c l } \lim \limits_{x \downarrow 2}l(2) & = & \infty \\ \end{array} \)
\(\\\)
Der Pol wird berechnet mit
\(\\\)
\( \quad \begin{array}{ r c l l } N(x) & = & 0 \\ x - 2 & = & 0 & | \, +2 \\ x_p & = & 2 \\ \end{array} \)
\(\\\)
Nicht immer muss \(N(x)=0\) eine Polstelle ergeben. Die Ausnahme bildet die hebbare Lücke.
\(\\[1em]\)
Hebbare Lücke
Hebbare Lücken sind Stellen, an denen die Voraussetzungen für Stetigkeit gegeben sind bis auf die Tatsache, dass diese Stelle nicht definiert ist.
\(\\\)
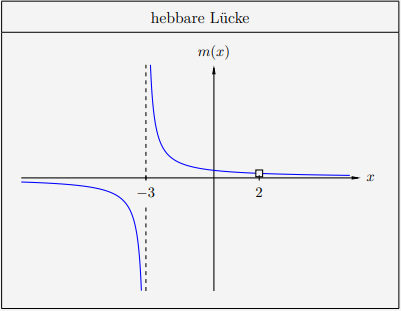
In diesem Fall liegt bei \(x_0=2\) eine hebbare Lücke vor. Wie hier zu sehen ist, existiert die Umgebung von \(x_0\) und ebenso der Grenzwert \(\lim \limits_{x \to x_0}=f(x_0)\).
Rechnerisch gilt nun:
Lässt sich die Lösung von \(N(x)=0\) mit \(x_0\) durch kürzen beseitigen, so handelt es sich um eine hebbare Lücke. Anders ausgedrückt:
Ist \(x_0\) eine Lösung von \(N(x)=0\) und von \(Z(x)=0\), so ist \(x_0\) eine hebbare Lücke.
\(\\\)
Betrachten wir nun die Funktion \(m\) mit
\(\\\)
\( \quad m(x) \; = \; \frac{x-2}{(x-2) \cdot (x+3)} \)
\(\\\)
Es ergibt sich mit
\(\\\)
\( \quad x-2=0 \iff x=2 \)
\(\\\)
und
\(\\\)
\( \quad (x-2) \cdot (x+3)=0 \iff x=2 \, \wedge \, x=-3 \)
\(\\\)
Da \(x=2\) sowohl um Zähler als auch im Nenner eine Lösung ist, muss dort eine hebbare Lücke sein. Bei \(x=-3\) liegt dagegen eine Polstelle. Beide Stellen sind nicht definiert. Es gilt der Definitionsbereich
\(\\\)
\( \quad \mathbb{D} \; = \; \mathbb{R} \setminus \{ -3, 2 \} \)
\(\\[1em]\)