HMF 7 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – P(X=4) = P(X=10)
Beim Wurf zweier Würfel ist die Wahrscheinlichkeit eines Elementarereignisses
\(\quad \{ (1;1), \; (1;2), \; (1;3), \; (1;4), \; \dots , \; (6;4), \; (6;5), \; (6;6) \} \)
stets gleich. Insgesamt gibt es 36 solcher Elementarereignisse.
\(\\\)
\(\\\)
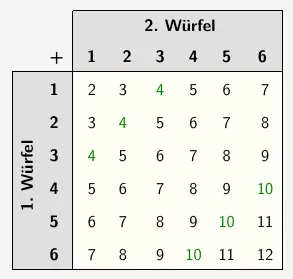
Jeweils 3 davon haben die Augensumme \(4\) bzw. \(10\) als Ergebnis.
\(\quad \begin{array}{ r c l } \text{Augensumme ist 4} & = & \{ (1;3), \; (2;2), \; (3;1) \} \\[5pt] \text{Augensumme ist 10} & = & \{ (4;6), \; (5;5), \; (6;4) \} \\ \end{array} \)
\(\\\)
Folglich haben beide Ereignisse die Wahrscheinlichkeit
\(\quad \begin{array}{ r c l c l } P(X=4) = P(X=10) & = & \frac{3}{36} & = & \frac{1}{12} \end{array} \)
\(\\[2em]\)
Aufgabe 2 – Diagramme
Für die Zufallsgröße \(X\) liegt der Erwartungswert, also der \(x\)-Wert mit der höchsten Wahrscheinlichkeit,

bei \(X=7\). Die Tabelle zeigt, dass
\(\quad \begin{array}{ r c l c l c l c l } P(X=7) & = & \frac{6}{36} & = & \frac{1}{6} & < & \frac{1}{5} & = & 0{,}2 \end{array} \)
\(\\\)
ist. Demnach kommt für die Zufallsgröße \(X\) nur das Diagramm \(\textrm{II}\) infrage.
Bei der Zufallsgröße \(Y\) handelt es sich um ein Zufallsversuch mit Zurücklegen und den beiden Merkmalsausprägungen schwarz und weiß. Folglich ist \(Y\) binomialverteilt.
Die Berechnung der Wahrscheinlichkeiten mit
\(\quad \begin{array}{ l } P(X=k) \, = \, \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k} \end{array} \)
sind ohne Hilfsmittel nicht zu bewerkstelligen (zumindest ist es mir nicht geglückt).
Es bleibt nur der Vergleich der Konturen der Verteilungen, hier als Punkteverteilung dargestellt.

Auffallend ist, dass Diagramm \(\textrm{I}\) und \(\textrm{II}\), zumindest näherungsweise, eine Dreiecksform bilden. Nur Diagramm \(\textrm{III}\) hat die für eine Binomialverteilung typische Glockenform. Zufallsgröße \(Y\) muss demnach Diagramm \(\textrm{III}\) zugeordnet werden.
\(\\\)