Aufgaben
Inhaltsverzeichnis
\(\\\)
“Buggy”
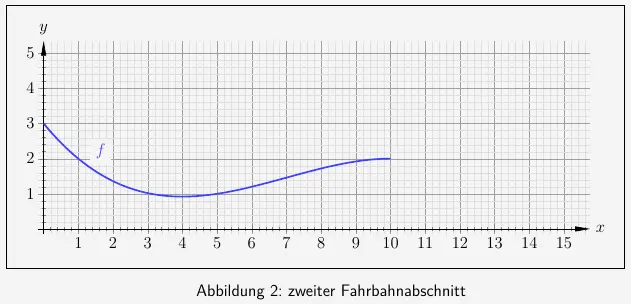
Mit ferngesteuerten Fahrzeugen, sogenannten Buggys, werden Rennen auf speziellen Fahrbahnen gefahren. Ein erster Fahrbahnabschnitt vom Startpunkt \(S\) zum Punkt \(P\) wird mithilfe einer Funktion \(f\) modelliert. An der Stelle \(x\) gibt \(f(x)\) die Höhe der Fahrbahn an. Auf beiden Achsen im zugehörigen Koordinatensystem entspricht eine Längeneinheit einem Meter in der Wirklichkeit.

\(\\[1em]\)
Abbildung
- Geben Sie mithilfe des Graphen die Höhe der Fahrbahn an der Stelle \(x=1\) an.
(1 P)
\(\\\)
-
Bestimmen Sie unter Verwendung geeigneter Hilfslinien in der Abbildung
-
die Stellen, an denen die Fahrbahnhöhe \(1{,}6\) beträgt, und \(\\\)
-
die Steigung der Fahrbahn an der Stelle \(x=2\).
(5 P)
-
\(\\[2em]\)
Funktion f
Verwenden Sie für den ersten Fahrbahnabschnitt im Folgenden
\( \quad f(x) \; = \; -0{,}01x^3 + 0{,}21x^2 - 1{,}2x + 3 \quad \text{mit} \quad x\in [0 ; 10] . \)
\(\\\)
Ein Buggy fährt von \(S(0|3)\) nach \(P(10|2)\). Während der Fahrt nimmt die Höhe der Fahrbahn zunächst ab, bis sie ihren Minimalwert erreicht, und nimmt anschließend wieder zu.
\(\\\)
- Berechnen Sie die minimale Höhe der Fahrbahn.
(4 P)
\(\\\)
- Berechnen Sie die maximale Steigung, die der Buggy während seiner Fahrt überwindet.
(5 P)
\(\\\)
-
Die Länge \(l\) des Graphen der Funktion \(f\) über dem Intervall \([a ; b]\) kann durch
\( \qquad l \; = \; \displaystyle{\int}_a^b \sqrt{1 + \left(f'(x)\right)^2} \)
berechnet werden. Berechnen Sie die Länge des Fahrbahnabschnitts.
(3 P)
\(\\[2em]\)
Funktion g
Ein zweiter Fahrbahnabschnitt wird durch die Funktion \(g\) mit
\( \quad g(x) \; = \; 2 \cdot e^{-0{,}4 \cdot (x - 10)^2} \quad \text{und} \quad x\in [10 ; 14] \)
\(\\\)
modelliert. An der Stelle \(x\) gibt \(g(x)\) die Höhe der Fahrbahn an.

\(\qquad \qquad \qquad \quad\)
\(\\\)
- Zeichnen Sie in die Abbildung 2 den Graphen der Funktion \(g\) unter Verwendung der angegebenen Tabelle.
(2 P)
\(\\\)
- Bestimmen Sie einen Term der ersten Ableitungsfunktion \(g'\) von \(g\)
(2 P)
\(\\\)
-
Der Graph von \(g\) schließt im Punkt \(P(10|2)\) an den Graphen von \(f\) an.
Untersuchen Sie, ob dieser Anschluss knickfrei ist.
(2 P)
\(\\\)
-
Für jedes \(a \in \mathbb{R}\) ist die Funktion \(g_a\) mit
\( \qquad g_a(x) \; = \; 2 \cdot e^{-a \cdot (x - 10)^2} \quad \text{und} \quad x\in [10 ; 14] \)
gegeben.
-
Weisen Sie nach, dass alle Funktionsgraphen der Schar durch den Punkt \(P(10|2)\) verlaufen.
-
Zeigen Sie, dass Punkt \(P\) der einzige Punkt ist, den je zwei verschiedene Graphen der Schar gemeinsam haben.
(5 P)
-
\(\\[2em]\)
Funktion h
Ein Buggy fährt mit so hoher Geschwindigkeit, dass er am Übergang der beiden Fahrbahnabschnitte an der Stelle \(x=10\) den Kontakt zur Fahrbahn verliert und ein Stück fliegt, bis er auf der durch \(g\) modellierten Fahrbahn landet und weiterfährt.
Die Flugbahn lässt sich mithilfe einer Parabel beschreiben. Diese besitzt den Scheitelpunkt \(P(10|2)\) und schneidet den Graphen von \(g\) an der Stelle \(x=12{,}3\).
-
Leiten Sie einen Funktionsterm der Funktion \(h\) her, deren Graph diese Parabel ist.
\( \qquad \big[\text{Kontrolle: } \; h(x) \approx -0{,}3325x^2 + 6{,}65x - 31{,}25 \big] \)
(4 P)
\(\\\)
- Berechnen Sie die durchschnittliche Höhe der Flugbahn über der Fahrbahn.
)
(3 P)
\(\\\)
-
Im Allgemeinen hängen die Weite der Fluges und die Geschwindigkeit \(v\) des Buggys an der Stelle \(x=10\), an der dieser den Kontakt zur Fahrbahn verliert, voneinander ab. Die zugehörige Flugbahn wird für \(v>0\) beschrieben mithilfe einer Parabel mit dem Funktionsterm
\( \qquad h_v(x) \; = \; -\frac{5}{v^2} (x-10)^2 + 2 . \)
\(\\\)
Diese Parabel schneidet den Graphen von \(g\) an der Stelle \(x=10+k\) mit \(0<k<4\).
Zeigen Sie, dass\( \qquad v \; = \; -\sqrt{\dfrac{5k^2}{2 - 2 \cdot e^{0{,}4k^2}}} \)
gilt.
(4 P)
\(\\[2em]\)