Aussagen
Inhaltsverzeichnis
\(\\\)
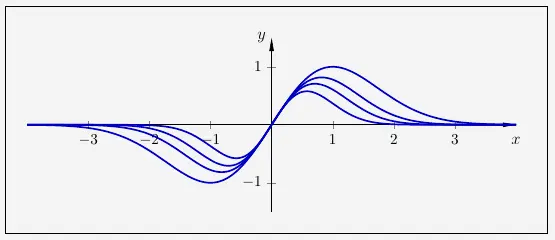
Aufgabe 1 – Verlauf der Graphen
Alle Graphen der Schar gehen durch den Koordinatenursprung und haben dort die gleiche Steigung. Außerdem gibt es keine andere Stelle, an der sich zwei verschiedene Graphen der Schar schneiden.
Bildlich sieht das dann folgendermaßen aus:
\(\\[2em]\)
Aufgabe 2 – Streckung der Schar
Streckung in y-Richtung
Wird eine Funktion in \(y\)-Richtung gestreckt oder gestaucht, so befindet sich der Streckungsfaktor vor der Funktion. Weiter gilt:
-
Ist der Streckungsfaktor größer als \(1\), so handelt es sich um eine Streckung.
-
Ist der Streckungsfaktor kleiner als \(1\), so handelt es sich um eine Stauchung.
\(\\[1em]\)
Streckung in x-Richtung
Wird eine Funktion in \(x\)-Richtung gestreckt oder gestaucht, so befindet sich der Streckungsfaktor vor dem \(x\). Weiter gilt:
-
Ist der Streckungsfaktor größer als \(1\), so handelt es sich um eine Stauchung.
-
Ist der Streckungsfaktor kleiner als \(1\), so handelt es sich um eine Streckung.
-
Ist der Streckungsfaktor bekannt, mit dem die \(e\)-Funktion gestaucht wird, und soll die Funktion mit dem gleichen Faktor jetzt gestreckt werden, so ist der Streckungsfaktor genau der Kehrwert dieses Faktors.
\(\\[1em]\)
Aufstellen der Gleichung
Wir definieren die Funktion
\( \quad f_a(x) \; = \; x \cdot e^{-\frac{1}{2} a \cdot x^2 + \frac{1}{2}} \)
\(\\\)
als Funktion \(h\) mit

Aus den obigen Beschreibungen folgt, dass der Streckungsfaktor in \(y\)-Richtung \(k\) ist und in \(x\)-Richtung der Faktor \(\frac{1}{k}\) sein muss.
Wir berechnen die gestreckte Funktion mit

Die Funktion
\( \quad \begin{array}{ r c l } f_{a,k}(x) & = & x \cdot e^{\frac{-a \cdot k^{-2} \cdot x^2}{2} + \frac{1}{2}} \\[6pt] & = & x \cdot e^{-\frac{a \cdot x^2}{2k^2} + \frac{1}{2}} \\[6pt] & = & x \cdot e^{-\frac{1}{2} \frac{a}{k^2} \cdot x^2 + \frac{1}{2}} \\ \end{array} \)
\(\\\)
ist eine Funktion der Schar \(f_a\), denn \(\frac{a}{k^2}\) mit \(k>0\) ist ebenfalls ein Wert von \(a\).
\(\\[1em]\)
Überprüfung
Überprüfen wir nun anhand von zwei Punkten die Funktion \(f_{a,k}\) mit verschiedenen \(k\)-Werten im Graphikmodus,

so können wir erkennen, dass es sich hier tatsächlich um gestreckte Funktionen mit dem gleichen Streckungsfaktor für beide Achsrichtungen handelt.
Damit kann die Aussage in der Aufgabenstellung bestätigt werden.
\(\\[2em]\)
Aufgabe 3 – Wendestellen
Mit dem Nullprodukt gibt es bei
\(\quad (a \cdot x^2 -3) \cdot x \; = \; 0 \)
\(\\\)
die Lösung \(x_1=0\). Weitere mögliche Lösungen sind in der Gleichung
\(\quad a \cdot x^2 -3 \; = \; 0 \)
\(\\\)
enthalten. Wir lösen die Gleichung nach \(x\) auf.
\( \quad \begin{array}{ r c l l } a \cdot x^2 -3 & = & 0 & | \, +3 \\[6pt] a \cdot x^2 & = & 3 & | \, :a \\[6pt] x^2 & = & \frac{3}{a} & | \, \sqrt{\dots} \\[8pt] x_2 & = & \sqrt{\frac{3}{a}} & \\[8pt] x_3 & = & -\sqrt{\frac{3}{a}} & \\ \end{array} \)
\(\\\)
Es sind nun zwei Fälle zu unterscheiden; \(a>0\) und \(a<0\). Ist \(a\) positiv (\(a>0\)), so sind alle \(x\) möglich und es gibt \(3\) Wendestellen. Ist \(a<0\), also negativ, so kann die Wurzel aus \(\frac{3}{a}\) nicht gezogen werden und es gibt nur eine Wendestelle bei \(x=0\).
\(\\\)