Untersuchung der Kontur
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Tiefpunkt
Wir definieren zunächst die Funktion \(f\).
Beachte: Der Mal-Punkt muss bei der Definition mitgeschrieben werden.

Für Extrempunkte gilt die
\(\\[1em]\)
Notwendige Bedingung
\(\quad f'(x) = 0 \)
\(\\\)
Die Ableitung bilden wir mit dem Werkzeug

\(\\\)
und erhalten dann die 1. Ableitung:

\(\\\)
Zum Lösen der Gleichung verwenden wir den Solve-Befehl:

\(\\\)
Zum Überprüfen der Art des Extrempunktes benötigen wir die
\(\\[1em]\)
Hinreichende Bedingung
\(\quad f''(x) = 0 \)
Dazu bilden wir die 2. Ableitung mit

\(\\\)
und überprüfen die \(x\)-Werte.

\(\\\)
\(\quad \begin{array}{ l c l } f''(0) & < & 0 \quad \Rightarrow \quad \textrm{Hochpunkt} \\[5pt] f''(3) & > & 0 \quad \Rightarrow \quad \textrm{Tiefpunkt} \\[5pt] f''(6) & < & 0 \quad \Rightarrow \quad \textrm{Hochpunkt} \end{array} \)
\(\\[1em]\)
Funktionswert

Der Tiefpunkt hat die Koordinaten \(( 3 | 1{,}028 )\).
\(\\[2em]\)
Aufgabe 2 – Graph von f
Um den Graphen zu zeichnen markieren wir den Funktionsterm von \(f\)

\(\\\)
und kopieren ihn mit
\(\\\)
Mit diesem Symbol

wechseln wir in den Graphik-Modus. Wir wählen

\(\\\)
und füge den Term mit
ein.

\(\\\)
Um den Graphen zu zeichnen, klicken wir das Feld vor \(Y1\) an.

\(\\\)
Es erscheint der Graph.

\(\\\)
Um einen besseren Bildausschnitt zu erhalten wählen wir dieses Symbol.

\(\\\)
Funktion \(f\) hat den Definitionsbereich \([0;6]\). Wir wählen als Zeichenbereich \(x \in [-0{,}5;6{,}5]\) und \(y \in [-1;4]\)

\(\\\)
und erhalten folgende Darstellung.

\(\\\)
Um den Graphen von \(f\) optimal zeichnen zu können erstellen wir eine Wertetabelle mit

\(\\\)
Wir brauchen die \(x\)-Werte von \(0\) bis \(6\).

\(\\\)
Mit dem Pfeil runter sehen wir auch den letzten Wert. wir übertragen Die Punkte in die Zeichnung und skizzieren den Graphen.
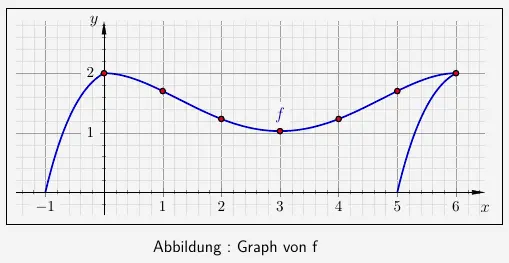
\(\\[2em]\)
Aufgabe 3 – Breite von 3 Dezimetern
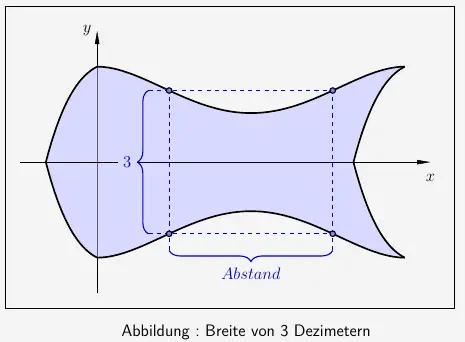
\(\\\)

\(\\\)
Nur \(x_2 =1{,}404685687\) und \(x_3 =4{,}595314313\) liegen innerhalb des Definitionsbereichs mit
\(\quad \mathbb{D} = \{ x \in \mathbb{R} \, \big| \, 0 \leq x \leq 6 \} \)
\(\\\)
Folglich beträgt der gesuchte
\(\quad Abstand \; = \; x_3 - x_2 \; = \; 4{,}595314313 - 1{,}404685687 \; \approx \; 3{,}19 \, dm \)
\(\\\)