Extrempunkte und Wendepunkte
Inhaltsverzeichnis
\(\\\)
Extrempunkte
Tangente
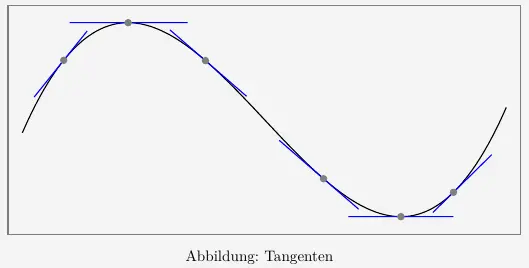
Eine Tangente ist eine Gerade, die den Graphen berührt (tangiert). Das heißt das die Tangente eine bestimmte Lage (Winkel) zum Graphen im Berührpunkt habe muss. Andernfalls würde die Gerade den Graphen schneiden und keine Tangente mehr sein.
\(\quad\)
\(\\\)
Bei den Extrempunkten fällt auf, dass die Tangente genau horizontal verläuft. Das bedeutet, dass die Steigung \(m\) der Tangente Null sein muss. Genau das ist auch der Ansatz zum Berechnen der Extrempunkte.
Nehmen wir als Beispiel die Funktion \(f\) mit
\( \quad f(x) \; = \; \frac{1}{2}x^3 - 6x \)
\(\\\)
Wir ermitteln nun die Stellen, wo die Tangentensteigung Null ergibt. Man nennt dies auch die notwendige Bedingung der Extrempunktberechnung, also quasi die Voraussetzung eines Extrempunktes.
Die Steigung der Tangente wird mit der ersten Ableitung der Funktion \(f\) berechnet.
\(\\[2em]\)
Berechnung der Extrempunkte
Notwendige Bedingung
Es gilt nun \(f'(x) \; = \; 0\)
Wir benötigen zunächst die 1. Ableitung.
\( \quad \begin{array}{ r c l l } f'(x) & = & \frac{3}{2}x^2 - 6 \\[12pt] \frac{3}{2}x^2 - 6 & = & 0 & \bigl| \; +6 \\[6pt] \frac{3}{2}x^2 & = & 6 & \bigl| \; \cdot \frac{2}{3} \\[6pt] x^2 & = & 4 & \bigl| \; \sqrt{\dots} \\[6pt] x_1 & = & 2 & \\[5pt] x_2 & = & -2 & \\ \end{array} \)
\(\\\)
An den Stellen \(x=2\) und \(x=-2\) finden wir waagerechte Tangenten an den Graphen von \(f\). Heißt das nun, dass sich dort Extrempunkte befinden?
Nicht zwangsläufig,
\(\quad\)
\(\\\)
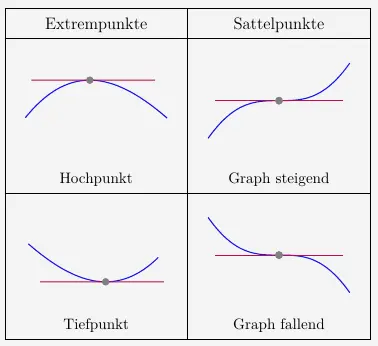
denn wie hier zu erkennen ist, gibt es auch andere Punkte die eine waagerechte Tangente besitzen, die Sattelpunkte (auch Terrassenpunkte genannt).
Das bedeutet, dass sich bei dem \(x\), wo \(f'(x)=0\) ist, nur möglicherweise ein Extrempunkt befindet. Ob hier tatsächlich ein Extrempunkt befindet und um welchen Extrempunkt es sich handelt, finden wir mit der hinreichenden Bedingung heraus.
\(\\[1em]\)
Hinreichenden Bedingung
Die hinreichende Bedingung kann nun auf zwei verschiedene Arten aufgestellt und angewendet werden. Beginnen wir mit der offensichtlicheren, wenn auch weniger gebräuchlichen Methode, da sie aufwändiger ist, an.
\(\\[1em]\)
Tangentensteigung
Betrachten wir unsere beiden Abbildungen, so lässt sich erkennen, das bezogen auf die mögliche Extremstelle beim
Hochpunkt → die Tangente davor steigend und danach fallend verläuft.
Tiefpunkt ⟶ die Tangente davor fallend und danach steigend verläuft.
Sattelpunkt → die Tangente entweder davor und danach steigend verläuft oder aber davor und danach fallend verläuft.
\(\\\)
Diese Eigenschaften verwenden wir nun mit einer neuen Aufgaben. Diese hat relativ krumme Zahlen zugunsten der Ergebnisse, die dann glatte Zahlen ergeben.
\( \quad f(x) \; = \; 0{,}09375 \cdot x^5 - 0{,}9375 \cdot x^4 + 3{,}125 \cdot x^3 - 3{,}75 \cdot x^2 + 4 \)
\(\\\)
Abgeleitet bekommen wir
\( \quad f'(x) \; = \; 0{,}46875 \cdot x^4 - 3{,}75 \cdot x^3 + 9{,}375 \cdot x^2 - 7{,}5 \cdot x \)
\(\\\)
Mit der notwendigen Bedingung \(f'(x) \; = \; 0\) erhalten wir
\( \quad 0 \; = \; 0{,}46875 \cdot x^4 - 3{,}75 \cdot x^3 + 9{,}375 \cdot x^2 - 7{,}5 \cdot x \)
\(\\\)
Dies ist quasi eine Nullstellenberechnung die wir mit dem Taschenrechner lösen, hier mit dem Casio fx-991DE X.
Wir gehen dazu auf
\(\\\)
und erhalten

\(\\\)
Wir wählen
\(\\\)

\(\\\)
und danach
\(\\\)
Weiter geben wir die Werte der Gleichung ein.

\(\\\)
Wir erhalten dann die Lösungen

\(\\\)

\(\\\)

\(\\\)
Wir überprüfen jeweils links und rechts die Tangentensteigungen bei den Werten \(0\), \(2\) und \(4\). Der Einfachheit halber nehmen wir ganzzahlige Werte. Wir brauchen also die Ableitungen an den Stellen \(-1\), \(1\), \(3\) und \(5\).
Wegen der Regelmäßigkeit der Abstände bietet sich hier eine Wertetabelle mit dem Taschenrechner an.
\(\\\)

\(\\\)
Nun geben wir die Funktion ein.

\(\\\)
Die zweite Funktion \(g(x)\) überspringen wir mit
\(\\\)
Im Tabellenbereich wählen wir als Startwert \(-1\)

\(\\\)
Für die Ableitung ergeben sich diese Werte

\(\\\)

\(\\\)
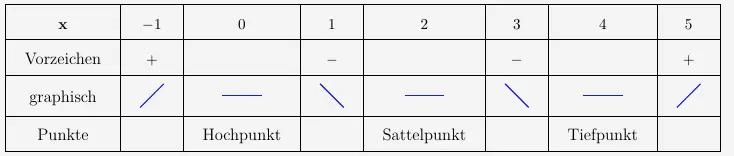
und damit folgendes Steigungsverhalten:
\(\\\)
Zusammenfassend kann man jetzt also sagen, dass wir die Art des Extrempunktes über den Vorzeichenwechsel der ersten Ableitung bestimmen.
Hochpunkt → Vorzeichenwechsel von plus nach minus.
Tiefpunkt ⟶ Vorzeichenwechsel von minus nach plus.
Sattelpunkt → keinen Vorzeichenwechsel
\(\\[1em]\)
Krümmung
Eine andere Möglichkeit, die mit Abstand die am meisten Verwendete, mit der hinreichenden Bedingung die Art der Extrempunkte herauszufinden, ist über die Krümmung an der möglichen Extremstelle.
\(\quad\)
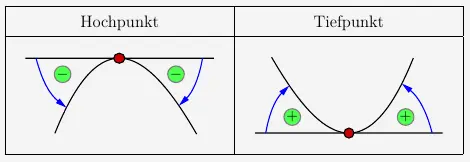
\(\\\)
Wie hier zu sehen ist, ist im Hochpunkt der Graph nach unten gekrümmt und hat damit eine negative Krümmung. Entsprechend ist im Tiefpunkt der Graph nach oben gekrümmt und hat eine positive Krümmung.
Die Krümmung wird mit der zweiten Ableitung bestimmt. Wir sagen nun:
-
Im Hochpunkt ist \(f''(x) \; < \; 0\) .
-
Im Tiefpunkt ist \(\; \; f'(x) \; > \; 0\) .
\(\\\)
Kommen wir nun zur Berechnung. Dazu nehmen wir wieder das Eingangsbeispiel auf. wir hatten die Gleichung
\( \quad f(x) \; = \; \frac{1}{2}x^3 - 6x \)
\(\\\)
mit der 1. Ableitung
\( \quad f'(x) \; = \; \frac{3}{2}x^2 - 6 \)
\(\\\)
und den möglichen Werten
\( \quad \begin{array}{ r c r } x_{_{E_1}} & = & 2 \\[5pt] x_{_{E_2}} & = & -2 \\ \end{array} \)
\(\\\)
Mit der hinreichenden Bedingung gilt nun
\( \quad f''(x_{_E}) \; \not= \; 0 \)
\(\\\)
Es gibt auch noch die Schreibweise \(f''(x_{_E}) \gtrless 0\).
Inhaltlich besagt sie das gleiche. Ich halte mich aber an die erste Schreibweise.
Wir bestimmen nun die 2. Ableitung
\( \quad f''(x) \; = \; 3x \)
\(\\\)
und überprüfen die \(x\)-Werte.
\( \quad \begin{array}{ c c c c r c l r l } f''(2) & = & 3 \cdot 2^2 & = & 12 & > & 0 & \quad \Rightarrow & \text{Tiefpunkt} \\[5pt] f''(-2) & = & 3 \cdot (-2)^2 & = & -12 & < & 0 & \quad \Rightarrow & \text{Hochpunkt} \\[5pt] \end{array} \)
\(\\[1em]\)
Linkskrümmung und Rechtskrümmung
Um die Eigenschaften der Extrempunkte einerseits zu vervollständigen und andererseits zur Überleitung zu den Wendepunkten, sei hier noch erwähnt, dass
\(\quad\)
\(\\\)
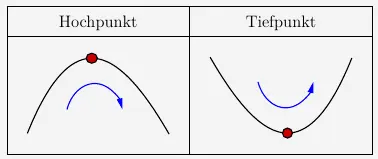
von links nach rechts betrachtet der Graph
-
im Hochpunkt im Uhrzeigersinn verläuft, also rechtsgekrümmt ist und
-
im Tiefpunkt gegen den Uhrzeigersinn verläuft, also linksgekrümmt ist.
\(\\[2em]\)
Wendepunkte
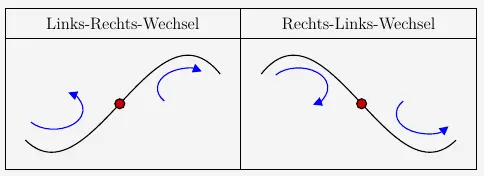
Die Wendestelle ist nun der \(x\)-Wert, bei dem der Graph der Funktion einen Wechsel von einer Linkskurve in eine Rechtskurve beschreibt oder eben anders herum.
\(\quad\)
\(\\\)
Wie wir zuvor schon festgestellt haben, bedeutet
-
eine Linkskurve eine positive Krümmung und
-
eine Rechtskurve eine negative Krümmung.
\(\\\)
Im Wendepunkt, der ja den Übergang von einer Krümmung in die andere ist, herrscht keine Krümmung vor. Daraus ergibt sich die notwendige Bedingung. Wir berechnen wieder die Krümmung mit der 2. Ableitung.
\(\\[1em]\)
Notwendige Bedingung
Es gilt \(f''(x) \; = \; 0\)
\(\\\)
Wir nehmen wieder das erste Beispiel, von dem wir ja bereits die 2. Ableitung
\( \quad f''(x) \; = \; 3x \)
\(\\\)
kennen und wenden die notwendigen Bedingung an.
\( \quad \begin{array}{ r c l l } 3x & = & 0 & | \; : 3 \\[6pt] x_{_W} & = & 0 \\ \end{array} \)
\(\\\)
Dies ist nun wieder der \(x\)-Wert einer möglichen Wendestelle. Ob hier tatsächlich eine Wendestelle vorliegt, wird mit der 3. Ableitung berechnet. Diese besagt nun Folgendes:
-
Liegt ein Links-Rechts-Wechsel vor, so ist \(f'''(x)<0\) .
-
Liegt ein Rechts-Links-Wechsel vor, so ist \(f'''(x)>0\) .
\(\\\)
Folglich liegt bei keinen Krümmungswechsel auch kein Wendepunkt vor. Das müssen wir ausschließen.
Denn bisher haben wir ja nur eine Stelle ohne Krümmung berechnet, aber noch keine Aussage zu den Krümmungswechsel an dieser Stelle.
\(\\[1em]\)
Hinreichende Bedingung
Es gilt \(f'''(x_{_W}) \; \not= \; 0\) .
\( \quad f'''(x_{_W}) \; = \; 3 \)
\(\\\)
Wir überprüfen nun \(x_{_W}\) .
\( \quad \begin{array}{ r c l l l } f'''(0) & = & 3 & > & 0 \\ \end{array} \)
\(\\\)
Es liegt ein Wendepunkt mit einem Rechts-Links-Wechsel vor.
\(\\[1em]\)
Größte Steigung und größtes Gefälle
Kommen wir nun abschließend bei den Wendepunkten zu einer wichtigen Eigenschaft.
\(\quad\)
\(\\\)
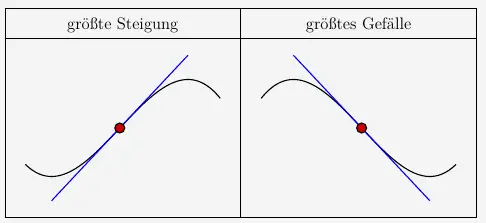
Zwischen zwei Extrempunkten liegt im Wendepunkte die größte Steigung oder aber das größte Gefälle vor.
Wird nun in einer Aufgabenstellung nach dem größten Gefälle oder der größten Steigung gefragt, so ist die Wendestelle zu berechnen.
\(\\[2em]\)
Sattelpunkte
Der Sattelpunkt wurde im Teil Tangentensteigung schon ausführlich behandelt. Wie wir gesehen haben, ist es ein Wendepunkt mit einer horizontalen Tangente. Entsprechend enthält der Sattelpunkt dann auch die Bedingungen für Extrempunkte und Wendepunkte.
\( \quad \begin{array}{ r r } \text{notwendige Bedingung:} & f'(x) \, = \, 0 \\[6pt] \text{hinreichende Bedingung:} & f''(x) \, = \, 0 \\ \end{array} \)
\(\\[2em]\)
Zusammenfassung

\(\\[2em]\)
Einfache Kurvendiskussion
Jetzt führen wir einmal die komplette Berechnung wie bei einer Kurvendiskussion durch, allerdings nur mit den Extrempunkten und Wendepunkte. Wir nehmen dazu das zweite Beispiel. Die Funktion lautet in der ursprünglichen Form
\( \quad f(x) \; = \; \frac{1}{32} \cdot \left(3 x^5 - 30 x^4 + 100 x^3 - 120 x^2 + 128 \right) \)
\(\\\)
Wir beginnen mit den Ableitungen. Dazu bietet es sich an, den Funktionsterm aus zu multiplizieren.
\( \quad \begin{array}{ r c l } f(x) & = & \frac{3}{32} x^5 - \frac{30}{32} x^4 + \frac{100}{32} x^3 - \frac{120}{32} x^2 + \frac{128}{32} \\[6pt] f(x) & = & \frac{3}{32} x^5 - \frac{15}{16} x^4 + \frac{25}{8} x^3 - \frac{15}{4} x^2 + 4 \\ \end{array} \)
\(\\\)
-
Ableitungen
\(\quad \begin{array}{ r c l } f'(x) & = & \frac{15}{32} x^4 - \frac{15}{4} x^3 + \frac{75}{8} x^2 - \frac{15}{2} x \\[8pt] f''(x) & = & \frac{15}{8} x^3 - \frac{45}{4} x^2 + \frac{75}{4} x - \frac{15}{2} \\[8pt] f'''(x) & = & \frac{45}{8} x^2 - \frac{45}{2} x + \frac{75}{4} \\ \end{array} \)
\(\\[1em]\)
-
Extrempunkte
-
Notwendige Bedingung: \(f'(x) = 0\)
\( \quad 0 \; = \; \frac{15}{32} x^4 - \frac{15}{4} x^3 + \frac{75}{8} x^2 - \frac{15}{2} x \)
\(\\\)
Wie man diese Gleichung mit dem Casio fx-991DE X löst, habe ich unter Tangentensteigung bereits gezeigt. Die Gleichung lässt sich aber auch mit einem Taschenrechner lösen, der nur Gleichungen 3. Grades lösen kann. Dazu verwenden wir das Nullprodukt. Wir klammern zunächst \(x\) aus.
\( \quad 0 \; = \; x \cdot \left( \frac{15}{32} x^3 - \frac{15}{4} x^2 + \frac{75}{8} x - \frac{15}{2} \right) \)
\(\\\)
Es gilt nun mit dem Nullprodukt
\( \quad x_1 \; = \; 0 \)
und
\( \quad \frac{15}{32} x^3 - \frac{15}{4} x^2 + \frac{75}{8} x - \frac{15}{2} \; = \; 0 \)
\(\\\)
Wir lösen die Gleichung mit dem Taschenrechner und bekommen
\( \begin{array}{ r c l } x_2 & = & 2 \\[5pt] x_3 & = & 4 \\ \end{array} \)
\(\\[1em]\)
-
Hinreichende Bedingung: \(f''(x) \not= 0\)
Wir überprüfen unsere Lösungen.
\( \begin{array}{ r c l r c c l } f''(0) & = & \frac{15}{8} \cdot 0^3 - \frac{45}{4} \cdot 0^2 + \frac{75}{4} \cdot 0 - \frac{15}{2} & = & - \frac{15}{2} & < & 0 \\[8pt] f''(2) & = & \frac{15}{8} \cdot 2^3 - \frac{45}{4} \cdot 2^2 + \frac{75}{4} \cdot 2 - \frac{15}{2} & = & 0 \\[8pt] f''(4) & = & \frac{15}{8} \cdot 4^3 - \frac{45}{4} \cdot 4^2 + \frac{75}{4} \cdot 4 - \frac{15}{2} & = & \frac{15}{2} & > & 0 \\ \end{array} \)
\(\\\)
-
An der Stelle \(x=0\) liegt an dem Graphen der Funktion eine horizontale Tangente an und hat der Graph eine negative Krümmung. Folglich liegt dort ein Hochpunkt.
-
An der Stelle \(x=2\) liegt an dem Graphen der Funktion eine horizontale Tangente an und hat der Graph keine Krümmung. Folglich liegt dort ein Sattelpunkt.
-
An der Stelle \(x=4\) liegt an dem Graphen der Funktion eine horizontale Tangente an und hat der Graph eine positive Krümmung. Folglich liegt dort ein Tiefpunkt.
\(\\[1em]\)
-
-
Funktionswert
Bisher haben wir nur die \(x\)-Werte untersucht. Die \(y\)-Werte fehlen noch. Diese berechnen wir mit den Funktionswerten.
\( \begin{array}{ r c l c l } f(0) & = & \frac{3}{32} \cdot 0^5 - \frac{15}{16} \cdot 0^4 + \frac{25}{8} \cdot 0^3 - \frac{15}{4} \cdot 0^2 + 4 & = & 4\\[8pt] f(2) & = & \frac{3}{32} \cdot 2^5 - \frac{15}{16} \cdot 2^4 + \frac{25}{8} \cdot 2^3 - \frac{15}{4} \cdot 2^2 + 4 & = & 2 \\[8pt] f(4) & = & \frac{3}{32} \cdot 4^5 - \frac{15}{16} \cdot 4^4 + \frac{25}{8} \cdot 4^3 - \frac{15}{4} \cdot 4^2 + 4 & = & 0 \\ \end{array} \)
\(\\\)
Damit erhalten wir die Punkte
\( \begin{array}{ l } H(0|4) \; {,} \quad S(2|2) \; {,} \quad T(4|0) \\ \end{array} \)
\(\\[2em]\)
-
-
Wendepunkte
Für Wendepunkte darf keine Krümmung vorliegen.
\(\\\)
Notwendige Bedingung: \(f''(x) = 0\)
Es gilt
\(\quad 0 \; = \; \frac{15}{8} x^3 - \frac{45}{4} x^2 + \frac{75}{4} x - \frac{15}{2} \)
\(\\\)
Zu Fuß ist diese Gleichung nur mit erheblichen Aufwand zu lösen, nämlich mit einem Näherungsverfahren. Wir lösen wieder mit dem Taschenrechner und erhalten
\( \begin{array}{ r c l l } x_{W_1} & = & 2 \\[5pt] x_{W_2} & = & 2 - \sqrt{2} & \approx 0{,}5858 \\[6pt] x_{W_3} & = & 2 + \sqrt{2} & \approx 3{,}4142 \\[5pt] \end{array} \)
\(\\\)
Bei \(x=2\) liegt der Sattelpunkt \(S(2|2)\). Diesen brauchen wir nicht weiter untersuchen.
\(\\[1em]\)
-
Hinreichende Bedingung: \(f'''(x) \not= 0\)
Für Wendepunkte muss ein Krümmungswechsel vorliegen. Wir überprüfen dies nun.
\( \begin{array}{ r c l r c c l } f''' \left( 2 - \sqrt{2} \right) & = & \frac{45}{8} \cdot \left( 2 - \sqrt{2} \right)^2 - \frac{45}{2} \cdot \left( 2 - \sqrt{2} \right) + \frac{75}{4} & = & \frac{15}{2} & > & 0 \\[8pt] f''' \left( 2 + \sqrt{2} \right) & = & \frac{45}{8} \cdot \left( 2 + \sqrt{2} \right)^2 - \frac{45}{2} \cdot \left( 2 + \sqrt{2} \right) + \frac{75}{4} & = & \frac{15}{2} & > & 0 \\ \end{array} \)
\(\\\)
Sowohl an der Stelle \(x=2 - \sqrt{2}\) als auch an der Stelle \(x=2 + \sqrt{2}\) hat der Graph einen Wechsel von einer Rechtskurve in eine Linkskurve.
\(\\[1em]\)
-
Funktionswerte
\( \begin{array}{ r c l c l c l } f\left( 2 - \sqrt{2} \right) & = & \frac{3}{32} \cdot \left( 2 - \sqrt{2} \right)^5 - \frac{15}{16} \cdot \left( 2 - \sqrt{2} \right)^4 + \frac{25}{8} \cdot \left( 2 - \sqrt{2} \right)^3 - \frac{15}{4} \cdot \left( 2 - \sqrt{2}\right)^2+4 & = & 3{,}237 \\[8pt] f\left( 2 + \sqrt{2} \right) & = & \frac{3}{32} \cdot \left( 2 + \sqrt{2} \right)^5 - \frac{15}{16} \cdot \left( 2 + \sqrt{2} \right)^4 + \frac{25}{8} \cdot \left( 2+ \sqrt{2} \right)^3 - \frac{15}{4} \cdot \left( 2 + \sqrt{2} \right)^2 +4 & = & 0{,}763 \\ \end{array} \)
\(\\\)
Damit haben wir die Wendepunkt
\(W_1(0{,}586|3{,}237)\) und \(W_2(3{,}414|0{,}763)\)
\(\\[2em]\)
-
-
Graph zeichnen
Zum Schluß tragen wir die Punkte in ein Koordinatensystem ein und zeichnen den Graphen.
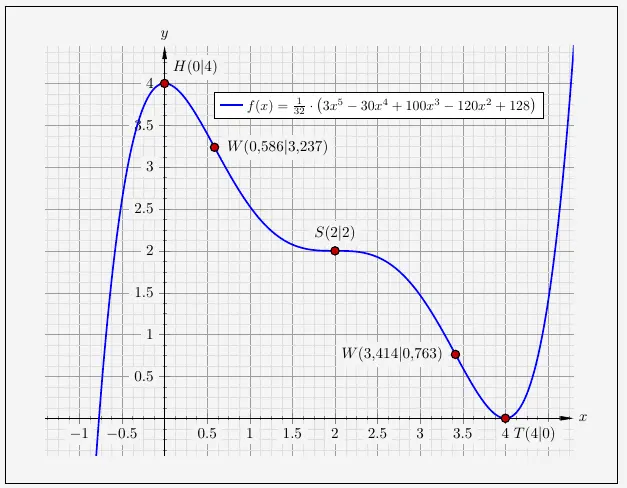
\(\\[1em]\)