Vergleich der Funktionen g und h
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – mittlere Steigung
Die mittlere Steigung wird berechnet mit
\( \quad m = \frac{f(x_2)-f(x_1)}{x_2 - x_1} \)
\(\\\)
Mit den Werten aus der Wertetabelle bekommen wir
\( \quad \begin{array}{ r c l } m_g & = & \frac{g(0)-g(-1)}{0- (-1)} \\[8pt] & = & \frac{0-2{,}5}{0+1} \\[8pt] & = & -2{,}5 \\ \end{array} \)
\(\\\)
Für \(m_h\) brauchen wir noch
\( \quad \begin{array}{ l*{5}{l} } h(0) & = & 5 \cdot 0^2 \cdot e^{\frac{2}{3} \cdot 0^3} & = & 0 \\[6pt] h(-1) & = & 5 \cdot (-1)^2 \cdot e^{\frac{2}{3} \cdot (-1)^3} & = & 2{,}567 \\ \end{array} \)
\(\\\)
Daraus folgt
\( \quad \begin{array}{ r c l } m_h & = & \frac{h(0)-h(-1)}{0- (-1)} \\[8pt] & = & \frac{0-2{,}567}{0+1} \\[8pt] & = & 2{,}567 \\ \end{array} \)
\(\\\)
Wir berechnen die prozentuale Abweichung bezüglich des Graphen von \(h\) . Das heißt, dass der Grundwert
\( \quad G=m_h=-2{,}567 \)
ist und der Prozentwert
\( \quad W=m_g=-2{,}5 \)
ist.
Wir berechnen den Prozentsatz \(p\) mit
\( \quad \begin{array}{ r c l } p & = & \frac{W \cdot 100\%}{G} \\[8pt] & = & \frac{-2{,}5 \cdot 100\%}{-2{,}567} \\[8pt] & = & 97{,}39\% \\ \end{array} \)
\(\\\)
Die prozentuale Abweichung ist also
\( \quad 100\% - 97{,}38\% = 2{,}61\% \)
\(\\[2em]\)
Aufgabe 2 – Lage der Graphen
Wenn
\( \quad h(1) - g(1) < 0 \)
\(\\\)
und
\( \quad h(2) - g(2) > 0 \)
\(\\\)
ist, dann folgt daraus, dass
\( \quad \Big( h(1) - g(1) \Big) \cdot \Big( h(2) - g(2) \Big) < 0 \; {,} \)
\(\\\)
also negativ ist.
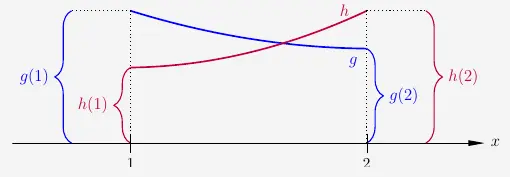
Das bedeutet, dass der Graph von \(g\) einmal oberhalb vom Graphen von \(h\) verläuft und einmal unterhalb vom Graphen von \(h\) .
\(\\\)
Daraus folgt, dass die Graphen von \(g\) und \(h\) im Bereich \(1<x<2\) einen Schnittpunkt haben müssen.
\(\\\)