Potenzregeln und Potenzgesetze
Inhaltsverzeichnis
\(\\\)
Was ist eine Potenz ?
Eine Potenz ist von der Gestalt
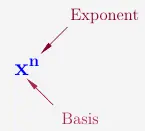
und drückt die Rechnung
\( \quad \underbrace{x \cdot x \cdot x \cdot x \dots x}_{\substack{n-mal}} \)
aus.
Es gilt die folgende Hierarchie der Rechenarten
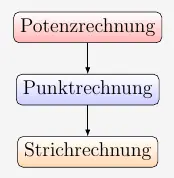
Das bedeutet:
- Punktrechnung vor Strichrechnung
- Potenzrechnung vor Punktrechnung
\(\\\)
Beispiel :
\( \quad \begin{array}{ r c c l } \textrm{richtig:} & 4 \cdot 2^3 & = & 4 \cdot 2 \cdot 2 \cdot 2 \; = \; 32 \\[6pt] \textrm{falsch:} & 4 \cdot 2^3 & = & (4 \cdot 2) \cdot (4 \cdot 2) \cdot (4 \cdot 2) \; = \; 512 \\[6pt] \textrm{jedoch:} & (4 \cdot 2)^3 & = & (4 \cdot 2) \cdot (4 \cdot 2) \cdot (4 \cdot 2) \; = \; 512 \quad \rightarrow \quad \textrm{richtig} \\ \end{array} \)
\(\\[2em]\)
Potenzgesetze
Potenzgesetz P1
Multiplikation mit gleicher Basis :
\( \quad \boxed{ x^m \cdot x^n \; = \; x^{m+n} } \)
\(\\\)
Beispiel :
\( \quad x^2 \cdot x^3 \; = \; \underbrace{x \cdot x}_{\substack{x^2}} \cdot \underbrace{x \cdot x \cdot x}_{\substack{x^3}} \; = \; x^{2 + 3} \)
\(\\\)
Division mit gleicher Basis :
\( \quad \boxed{ \begin{array}{ r c l } \displaystyle{\frac{x^m}{x^n}} & = & x^{m-n} \\ \end{array} } \)
\(\\\)
Beispiel :
\( \quad \dfrac{x^5}{x^3} \; = \; \dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x \cdot x} \; = \; \dfrac{x \cdot x \cdot \not{x} \cdot \not{x} \cdot \not{x}}{\not{x} \cdot \not{x} \cdot \not{x}} \; = \; x^2 \; = \; x^{5 - 3} \)
\(\\[2em]\)
Potenzgesetz P2
Multiplikation mit gleichem Exponenten :
\( \quad \boxed{ x^n \cdot y^n \; = \; (x \cdot y)^n } \)
\(\\\)
Beispiel :
\( \quad \begin{array}{ r c l } a^3 \cdot b^3 & = & a \cdot a \cdot a \cdot b \cdot b \cdot b \\[6pt] & = & a \cdot b \cdot a \cdot b \cdot a \cdot b \\[6pt] & = & (a \cdot b) \cdot (a \cdot b) \cdot (a \cdot b) \\[6pt] & = & (a \cdot b)^3 \\ \end{array} \)
\(\\\)
Division mit gleichem Exponenten:
\( \quad \boxed{ \frac{x^n}{y^n} \; = \; \left(\frac{x}{y}\right)^n } \)
\(\\\)
Beispiel zur Veranschaulichung :
\( \quad \dfrac{a^3}{b^3} \; = \; \dfrac{a \cdot a \cdot a}{b \cdot b \cdot b} \; = \; \dfrac{a}{b} \cdot \dfrac{a}{b} \cdot \dfrac{a}{b} \; = \; \left(\dfrac{a}{b}\right)^3 \)
\(\\[2em]\)
Potenzgesetz P3
Potenz einer Potenz :
\( \quad \boxed{ \left( x^m \right)^n \; = \; x^{m \cdot n} } \)
\(\\\)
Beispiel :
\( \quad \displaystyle{\left( x^3 \right)^2} \; = \; \underbrace{x \cdot x \cdot x}_{\substack{x^3}} \cdot \underbrace{x \cdot x \cdot x}_{\substack{x^3}} \; = \; x^{2 \cdot 3} \)
\(\\\)
Das Ganze lässt sich auch umdrehen:
\( \quad \displaystyle{\left( x^2 \right)^3} \; = \; \underbrace{x \cdot x}_{\substack{x^2}} \cdot \underbrace{x \cdot x}_{\substack{x^2}} \cdot \underbrace{x \cdot x}_{\substack{x^2}} \; = \; x^{3 \cdot 2} \)
\(\\\)
Dabei ist zu beachten, dass beispielsweise
\( \quad \displaystyle{e^{x^2}} \; \not= \; \displaystyle{\left( e^x \right)^2} \)
ist.
Vielmehr ist nach dem oben Dargestellten
\( \quad \displaystyle{\left( e^x \right)^2} \; = \; \displaystyle{e^{2x}} \)
\(\\\)
Und \(x^2 = 2x\) ist nur für die \(x\)-Werte \(x=0\) und \(x=2\) wahr, aber eben nicht generell.
\(\\[2em]\)
Potenzregeln
Exponent ist Null
Für alle \(x\) gilt
\( \quad \boxed{ x^0 \; = \; 1 } \)
\(\\[2em]\)
Potenzen mit negativem Exponenten
\( \quad \boxed{ \displaystyle{\frac{1}{x^n} \; = \; x^{-n} } } \)
\(\\\)
Als Bruch geschrieben wird ein negativer Exponent positiv, indem die Potenz vom Zähler in den Nenner oder auch umgekehrt geschrieben wird.
Dazu ein Beispiel zum Vereinfachen eines Bruches mit Potenzen, wobei die 3 Potenzgesetze ebenfalls angewendet werden:
\( \quad \begin{array}{ r c l l} \displaystyle{\left( \dfrac{x^4 \cdot y^{-3} \cdot z^{-5}}{x^3 \cdot y \cdot z^3} \right)^{-2}} & = & \displaystyle{\left( \dfrac{x^3 \cdot y \cdot z^3}{x^4 \cdot y^{-3} \cdot z^{-5}} \right)^2} & \quad \rightarrow \ddot{a}\text{ußerer Exponent positiv} \\[8pt] & = & \displaystyle{\left( \dfrac{y \cdot y^3 \cdot z^3 \cdot z^5}{x^4 \cdot x^{-3}} \right)^2} & \quad \rightarrow \text{gleiche Basen zusammen} \\[8pt] & = & \displaystyle{\left( \dfrac{y^{1 + 3} \cdot z^{3 + 5}}{x^{4 - 3}} \right)^2} & \quad \rightarrow \text{1. Potenzgesetz} \\[8pt] & = & \displaystyle{\left( \dfrac{y^4 \cdot z^8}{x} \right)^2} & \quad \rightarrow \text{Zusammenfassen} \\[8pt] & = & \displaystyle{\dfrac{\left(y^4 \right)^2 \cdot \left(z^8 \right)^2}{x^2}} & \quad \rightarrow \text{2. Potenzgesetz} \\[8pt] & = & \displaystyle{\dfrac{y^{2 \cdot 4} \cdot z^{2 \cdot 8}}{x^2}} & \quad \rightarrow \text{3. Potenzgesetz} \\[8pt] & = & \displaystyle{\dfrac{y^8 \cdot z^{16}}{x^2}} & \quad \rightarrow \text{Zusammenfassen} \\ \end{array} \)
\(\\[2em]\)
Wurzel als Potenz
Es gilt
\( \quad \boxed{ \displaystyle{\sqrt[n]{x^m} \; = \; x^{\frac{m}{n}}} } \)
\(\\\)
Dabei ist zu beachten :
- Ist bei der Wurzel kein Wurzelgrad angegeben, so ist \(n=2\).
- Ist bei dem \(x\) kein Exponent angegeben, so ist \(m=1\).
\(\\\)
Die Potenzschreibweise der Wurzeln wird häufig bei Ableitungen benötigt. Dazu folgt ein ausführliches Beispiel.
\(\\[2em]\)
Ableiten von Wurzeln
Die Funktion
\( \quad f(x) \; = \; 5 \displaystyle{\sqrt[7]{x^3}} \)
\(\\\)
kann in dieser Schreibweise nicht abgeleitet werden. Dazu muss \(f(x)\) in der Form
\( \quad f(x) \; = \; ax^n \)
\(\\\)
vorliegen. Das erreichen wir mit der Potenzschreibweise des Wurzelausdrucks.
\( \quad f(x) \; = \; 5\displaystyle{x^{\frac{3}{7}}} \)
\(\\\)
Abgeleitet erhalten wir
\( \quad f'(x) \; = \; \frac{15}{7}\displaystyle{x^{\frac{3}{7}-1}} \)
\(\\\)
Bei einer Subtraktion von Brüche benötigen wir zwei Brüche mit gleichem Nenner und schreiben
\( \quad f'(x) \; = \; \frac{15}{7}\displaystyle{x^{\frac{3}{7} - \frac{7}{7}}} \; = \; \frac{15}{7}\displaystyle{x^{- \frac{4}{7}}} \)
\(\\\)
Um von der Potenzschreibweise wieder in die Wurzelschreibweise zu kommen, wird zunächst der negative Exponent aufgelöst
\( \quad \displaystyle{f'(x) \; = \; \frac{15}{7} \cdot \frac{1}{x^{\frac{4}{7}}}} \)
\(\\\)
und weiter in die Wurzelschreibweise umgeformt.
\( \quad \displaystyle{f'(x) \; = \; \frac{15}{7} \cdot \frac{1}{\sqrt[7]{x^4}}} \; = \; \displaystyle{\frac{15}{7 \sqrt[7]{x^4}}} \)
\(\\\)
Alles zusammen sieht dann folgendermaßen aus:
\( \quad \begin{array}{ r c l } \displaystyle{f(x)} & = & \displaystyle{5 \sqrt[7]{x^3} \; = \; 5 x^{\frac{3}{7}}} \\[8pt] \displaystyle{f'(x)} & = & \frac{15}{7}\displaystyle{x^{\frac{3}{7}-1} \; = \; \frac{15}{7} x^{\frac{3}{7} - \frac{7}{7}} \; = \; \frac{15}{7} x^{- \frac{4}{7}} \; = \; \frac{15}{7} \cdot \frac{1}{x^{\frac{4}{7}}} \; = \; \frac{15}{7} \cdot \frac{1}{\sqrt[7]{x^4}} \; = \; \frac{15}{7 \sqrt[7]{x^4}}} \\ \end{array} \)
\(\\[2em]\)
Zehnerpotenzen
Zehnerpotenzen mit positiven Exponenten
Bei den positiven Exponenten habe ich die Null mit aufgeführt.
\( \quad \begin{array}{ r c l c r } 10^0 & = & & & 1 \\[6pt] 10^1 & = & & & 10 \\[6pt] 10^2 & = & 10 \cdot 10 & = & 100 \\[6pt] 10^3 & = & 10 \cdot 10 \cdot 10 & = & 1000 \\[6pt] 10^4 & = & 10 \cdot 10 \cdot 10 \cdot 10 & = & 10000 \\ \end{array} \)
\(\\[2em]\)
Zehnerpotenzen mit negativem Exponenten
Es gilt die Regel für negative Exponenten
\( \quad \begin{array}{ r c l c r } 10^{-1} & = & \frac{1}{10^1} & = & \frac{1}{10} & = & 0{,}1 \\[6pt] 10^{-2} & = & \frac{1}{10^2} & = & \frac{1}{100} & = & 0{,}01 \\[6pt] 10^{-3} & = & \frac{1}{10^3} & = & \frac{1}{1000} & = & 0{,}001 \\[6pt] 10^{-4} & = & \frac{1}{10^4} & = & \frac{1}{10000} & = & 0{,}0001 \\ \end{array} \)
\(\\\)
Hier ist zu sehen, dass der negative Exponent die Nachkommastelle der \(1\) angibt.
\(\\[2em]\)
Beispiele aus der Physik
Lichtgeschwindigkeit:
\( \quad 3 \cdot 10^8 \, \frac{m}{s} \; = \; 300 000 000 \, \frac{m}{s} \)
\(\\[1em]\)
Masse eines Wasserstoffatoms:
\( \quad 1{,}67 \cdot 10^{-27} \, kg \; = \; 0{,}000 000 000 000 000 000 000 000 001 67 \; kg \)
\(\\[1em]\)