Aufgaben
Inhaltsverzeichnis
\(\\\)
“Deich”
Angesichts des vorhergesagten Anstiegs des Meeresspiegels wird an der Nordseeküste ein neuer Klimadeich geplant. Stellvertretend für den ganzen Deich wird ein ausgewählter Deichquerschnitt betrachtet, dessen obere Begrenzungslinie durch die Funktion \(f\) mit
\( \quad f(x) \; = \; -288 \cdot (x - 9) \cdot e^{-0{,}1 \cdot (x - 9)^2 - 6} \quad \textit{und} \quad 0 \leq x \leq 9 \)
modelliert wird. Im Folgenden entspricht dabei eine Längeneinheit sowohl in \(x\)- als auch in \(y\)-Richtung stets \(10 \, m\) in der Wirklichkeit.

\(A\) ist ein Bezugspunkt auf dem Deich, der zur Vermessung dient. \(H\) ist der höchste Punkt des Deiches.
\(\\[1em]\)
Funktion f
- Bestimmen Sie die Höhe des Punktes \(A\) und die Steigung des Deiches im Punkt \(A\).
(3 P)
\(\\\)
- Berechnen Sie die Breite des Deiches in einer Höhe von \(5 \; m\).
(3 P)
\(\\\)
- Berechnen Sie die Deichhöhe.
(4 P)
\(\\[2em]\)
Schar von g
Im Folgenden wird die Schar der Funktionen \(g_k\) mit
\( \quad g_k(x) \; = \; -8 \cdot k^2 \cdot (x - 9) \cdot e^{-0{,}1 \cdot (x - 9)^2 - k} \quad f\ddot{u}r \; k \in \mathbb{R} \; und \; 0 \leq x \leq 9 \)
betrachtet.
\(\\[1em]\)
- Zeigen Sie, dass \(f\) ein Element dieser Schar ist.
(2 P)
\(\\\)
- Begründen Sie anhand des Funktionsterms:
Für jedes \(k \not= 0\) hat \(g_k\) genau eine Nullstelle.
(2 P)
\(\\\)
Ein Planungsbüro modelliert mit Hilfe der Funktionen \(g_k\) die obere Begrenzungslinie von weiteren Deichquerschnitten. Dazu werden im Folgenden ausschließlich die Parameterwerte \(k\) mit \(5 \leq k \leq 7\) betrachtet.
\(\\\)
- Für jedes solches \(k\) ist
\( \qquad H_k\left( 9 - \sqrt{5} \, \Bigl| \, 8 \cdot \sqrt{\frac{5}{e}} \cdot k^2 \cdot e^{-k} \right) \)
der Hochpunkt des Graphen von \(g_k\). Die \(y\)-Koordinate von \(H_k\) entspricht der Deichhöhe.
- Bestimmen Sie denjenigen Wert für \(k\), für den die Deichhöhe \(11 \, m\) beträgt.
(2 P)
\(\\\)
- Berechnen Sie die Deichhöhe des höchsten Deiches, der mit Hilfe einer dieser Funktion \(g_k\) mit \(5 \leq k \leq 7\) modelliert werden kann.
(5 P)
\(\\\)
- Für jedes betrachtete \(k\) hat \(g_k\) im Intervall \(\left[0 \, ; \, 9 - \sqrt{15}\right]\) genau eine Wendestelle. Bestimmen Sie die Koordinaten des zugehörigen Wendepunkts.
\( \qquad \left[ \text{Kontrolle:} \quad \text{Die Wendestelle ist } \; 9 - \sqrt{5} \, \right] \)
(3 P)
\(\\\)
- Der Deich steigt seeseitig bis zu seinem höchsten Punkt an. Dabei verläuft das Deichprofil im Uferbereich zunächst flach, wird dann steiler und flacht zum höchsten Punkt hin wieder ab. Aus Stabilitätsgründen darf der maximale Steigungswinkel des Deichprofils seeseitig höchstens \(20^\circ\) betragen.
Untersuchen Sie, für welche \(k\) mit \(5 \leq k \leq 7\) diese Bedingung erfüllt ist.
(5 P)
\(\\[2em]\)
Deichkrone
Für die weitere Planung wird der durch \(g_{5{,}8}\) modellierte Deich ausgewählt. Dieser soll einen begradigten Bereich (die sogenannte Deichkrone) erhalten.
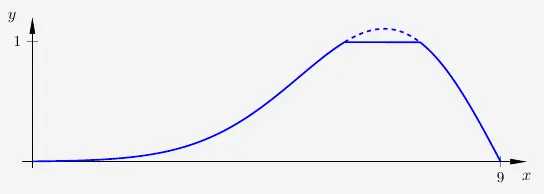
\(\\\)
- Ermitteln Sie rechnerisch die Höhe, in der der Deich begradigt werden müsste, damit die Deichkrone waagerecht und \(12 \, m\) breit ist.
(3 P)
\(\\\)
Es wird entschieden, den Deich für \(6{,}0 \leq x \leq 7{,}2\) zu begradigen.
\(\\\)
- Zeigen Sie, dass der Deich auf diese Weise nicht waagerecht begradigt wird.
Bestimmen Sie die Neigung des begradigten Bereichs in Prozent.
(3 P)
\(\\\)
- Ein Abschnitt des geplanten Deich soll \(2 \, km\) lang werden.
Berechnen Sie die Menge des benötigten Materials in Kubikmetern.
(5 P)
\(\\[2em]\)