Lineare Regression
Inhaltsverzeichnis
\(\\\)
1. bivariate Häufigkeitsverteilung
Die lineare Regression beschäftigte sich mit Maßen der bivariaten Häufigkeitsverteilung. Das heißt, das jedes Element zwei Merkmale besitzt.
Wir betrachten die Merkmale \(x\) als Körpergröße in Zentimeter und \(y\) als Körpergewicht in Kilogramm von \(12\) Personen.
Die Zählvariable sei \(i\).
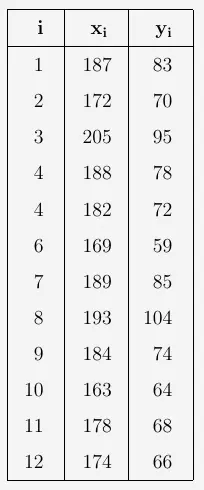
\(\\\)
Als Diagramm sieht die Verteilung folgendermaßen aus:
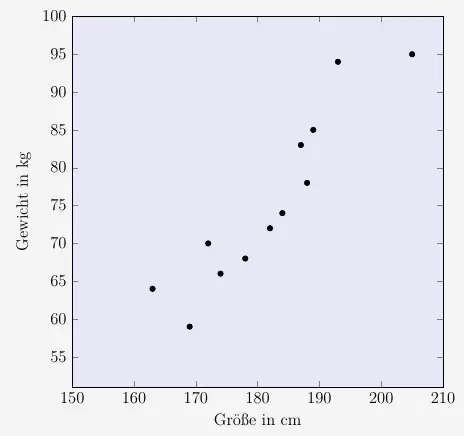
Gibt es nun einen Zusammenhang zwischen der Körpergröße einer Personen und deren Gewicht? Das Diagramm lässt die Vermutung aufkommen.
Wie kann man diesen Zusammenhang nun rechnerisch, also quasi per Formel, formulieren?
Offensichtlich steigt das Gewicht mit zunehmender Größe. Es liegt also nahe, diese Verteilung als Gerade anzunehmen.
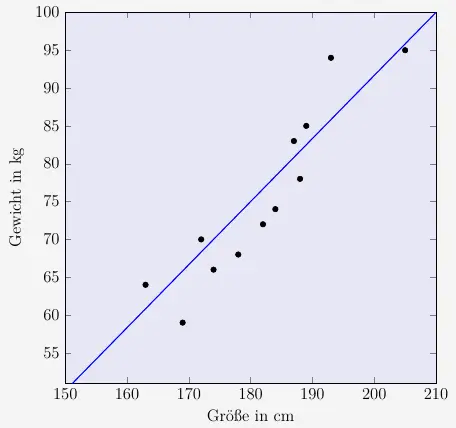
Eine repräsentative Gerade wäre die Regressionsgerade. Diese vorläufig eingezeichnete Gerade ist noch nicht die Regressionsgerade.
\(\\[2em]\)
2. Regressionsgerade
Welche Eigenschaft braucht die Regressionsgerade?
Damit sie die Verteilung gut repräsentiert, müsste die Summe der Abweichungsquadrate der einzelnen Punkte von der Geraden in \(y\)-Richtung möglichst klein sein, wie wir es ja schon in der Varianz und Standardabweichung angewendet haben.
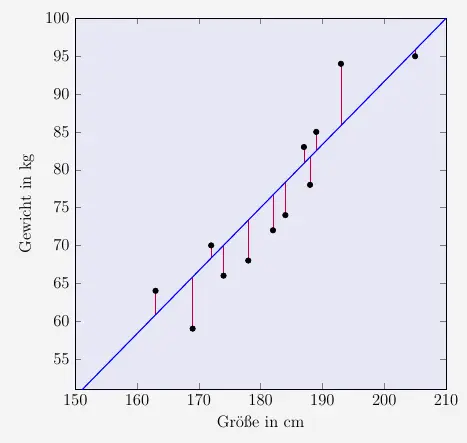
Wir gehen dabei von der Geradengleichung
\( \quad y = a + bx \)
\(\\\)
aus. Also berechnen sich die Abweichungen mit
\( \quad y_i - (a + bx_i) \qquad \text{mit} \quad i = \{1, \dots , n\} \)
\(\\[1em]\)
Kovarianz
Zur Berechnung benötigen wir die Kovarianz, die folgendermaßen ermittelt wird:
\( \quad s_{xy}=\overline{xy} - \overline{x} \cdot \overline{y} \)
\(\\\)
Ferner brauchen wir den Mittelwert \(\overline{xy}\) des Produktes \(x_i \cdot y_i\). Zusätzlich kommen noch die Quadrate der Tabellenwerte hinzu und wir berechnen nun wie folgt:

\(\\\)
Bei der Regressionsgeraden von der Form
\( \quad y = a + bx \)
\(\\\)
wird \(b\) berechnet mit
\( \quad b = \dfrac{s_{xy}}{s_x^2} \)
\(\\\)
Dabei ist
\( \quad \begin{array}{ r c l } s_{xy} & = & \frac{1}{n}\sum (x_i - \overline{x}) \cdot (y_i - \overline{y})\\[8pt] s_x^2 & = & \frac{1}{n}\sum (x_i - \overline{x})^2 \\[8pt] s_y^2 & = & \frac{1}{n}\sum (y_i - \overline{y})^2 \\ \end{array} \)
\(\\\)
Vereinfacht gilt nun, dass
\( \quad \begin{array}{ r c l } s_{xy} & = & \overline{xy} - \overline{x} \cdot \overline{y} \\[6pt] s_x^2 & = & \overline{x^2} - \overline{x}^2 \\[6pt] s_y^2 & = & \overline{y^2} - \overline{y}^2 \\ \end{array} \)
ist.
Daraus folgt, dass \(b\) berechnet werden kann mit
\( \quad b = \dfrac{\overline{xy} - \overline{x} \cdot \overline{y}}{\overline{x^2} - \overline{x}^2} \)
\(\\\)
Aus der Tabelle haben wir folgende Ergebnisse bekommen:
\( \quad \begin{array}{ r c l } n & = & 12 \\[6pt] \sum{x} & = & 2184 \\[6pt] \overline{x} & = & 182 \\[6pt] \sum{x^2} & = & 398962 \\[6pt] \overline{x^2} & = & 33246{,}83 \\[6pt] \sum{y} & = & 918 \\[6pt] \overline{y} & = & 76{,}5 \\[6pt] \sum{xy} & = & 168548 \\[6pt] \overline{xy} & = & 14045{,}67 \\ \end{array} \)
\(\\\)
Wir setzen diese Werte ein und erhalten
\( \quad b = \dfrac{14045{,}67 - 182 \cdot 76{,}5}{33246{,}83 - 182^2} = 0{,}9987 \)
\(\\\)
\(a\) ergibt sich mit
\( \quad a=\overline{y} - b \cdot \overline{x} \)
\(\\\)
Eingesetzt:
\( \quad a=76{,}5 - 0{,}9987 \cdot 182 = - 105{,}2634 \)
\(\\\)
Die Regressionsgerade lautet also
\( \quad y = 0{,}9987 x - 105{,}2634 \)
\(\\\)
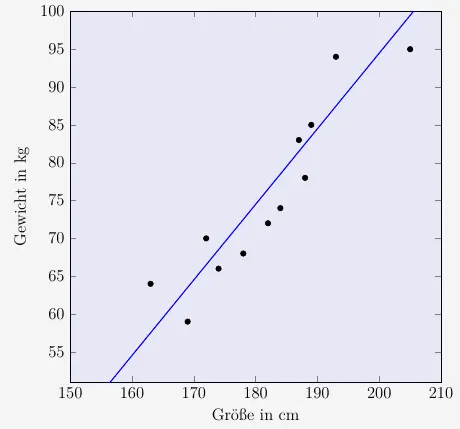
Um die Gerade darzustellen, ermitteln wir 2 \(y\)-Werte, zum Beispiel bei \(x=160\) und bei \(x=200\).
\( \quad \begin{array}{ r c c c l } y & = & 0{,}9987 \cdot 160 - 105{,}2634 & = & 54{,}5286 \\[6pt] y & = & 0{,}9987 \cdot 200 - 105{,}2634 & = & 94{,}4766 \\ \end{array} \)
\(\\\)
Wir erhalten also die Punkte \(P_1(160|54{,}53)\) und \(P_2(200|94{,}48)\) und zeichnen die Gerade.
\(\\[2em]\)
3. Umkehrregression
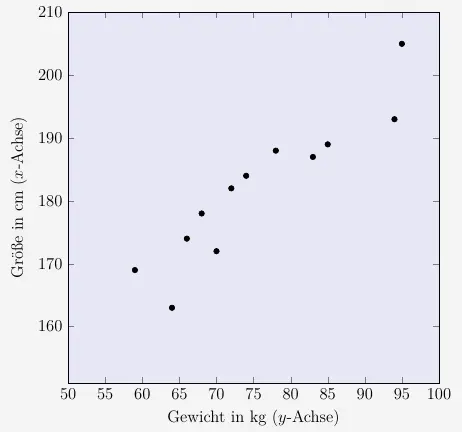
Wie sieht das Ganze nun umgekehrt aus? Also wie ist der Zusammenhang der Körpergröße zum Gewicht der untersuchten Personen?
Wir vertauschen die Achsen. Damit steht dann die unabhängige Variable \(y\) für das Gewicht und die abhängige Variable \(x\) für die Größe.
\(\\\)
Aus der Tabelle, hier noch einmal dargestellt,

\(\\\)
erhalten wir folgende Werte:
\( \quad \begin{array}{ r c l } n & = & 12 \\[6pt] \sum{x} & = & 2184 \\[6pt] \overline{x} & = & 182 \\[6pt] \sum{y} & = & 918 \\[6pt] \overline{y} & = & 76{,}5 \\[6pt] \sum{y^2} & = & 72156 \\[6pt] \overline{y^2} & = & 6013 \\[6pt] \sum{xy} & = & 168548 \\[6pt] \overline{xy} & = & 14045{,}67 \\ \end{array} \)
\(\\\)
Diesmal gehen wir von der Regressionsgeraden
\( \quad x = my + n \)
\(\\\)
aus. \(m\) wird berechnet mit
\( \quad m = \dfrac{s_{xy}}{s_y^2} = \dfrac{\overline{xy} - \overline{x} \cdot \overline{y}}{\overline{y^2} - \overline{y}^2} \)
\(\\\)
Eingesetzt erhalten wir
\( \quad m = \dfrac{14045{,}67 - 182 \cdot 76{,}5}{6013 - 76{,}5^2} = 0{,}76311 \)
\(\\\)
\(n\) ergibt sich mit
\( \quad n=\overline{x} - m \cdot \overline{y} \)
\(\\\)
Also
\( \quad n=182 - 0{,}76311 \cdot 76{,}5 = 123{,}6221 \)
\(\\\)
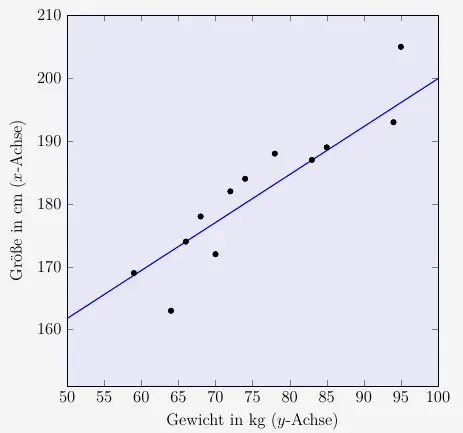
Die Regressionsgerade lautet also
\( \quad x = 0{,}76311 y + 123{,}6221 \)
\(\\\)
und stellt sich folgendermaßen dar:
\(\\[2em]\)
4. Korrelationskoeffizient
Nun stellt sich noch die Frage, ob diese Regressionsgerade die Punkteverteilung gut repräsentiert. Oder besser ausgedrückt:
Ist die Verteilung geeignet um als Gerade zu modelliert zu werden?
Ein Maß , dass die Güte dafür misst, ist der Korrelationskoeffizient.
\( \quad r_{xy} \; = \; \dfrac{s_{xy}}{s_x \cdot s_y} \)
\(\\\)
Vereinfacht sagen wir hier,
\( \quad r_{xy} \; = \; \dfrac{ \overline{xy} - \overline{x} \cdot \overline{y} }{ \sqrt{\left(\overline{x^2} - \overline{x}^2\right)} \cdot \sqrt{\left(\overline{y^2} - \overline{y}^2\right)} } \)
ist.
Mit den Werten
\( \quad \begin{array}{ r c l } \overline{x} & = & 182 \\[6pt] \overline{x^2} & = & 33246{,}83 \\[6pt] \overline{y} & = & 76{,}5 \\[6pt] \overline{y^2} & = & 6013 \\[6pt] \overline{xy} & = & 14045{,}67 \\ \end{array} \)
\(\\\)
erhalten wir
\( \quad r_{xy} \; = \; \dfrac{ 14045{,}67 - 182 \cdot 76{,}5 }{ \sqrt{\left(33246{,}83 - 182^2\right) \cdot \left(6013 - 76{,}5^2\right)} } \; = \; 0{,}873 \)
\(\\\)
Wie ist dieser Wert nun zu beurteilen?
Es gilt:
\( \quad \begin{array}{ c c l } 0 & = & \text{kein linearer Zusammenhang} \\[6pt] (0 ; 0{,}5] & = & \text{relativ schwacher linearer Zusammenhang} \\[6pt] (0{,}5 ; 0{,}8] & = & \text{mittlerer linearer Zusammenhang} \\[6pt] (0{,}8 ; 1) & = & \text{relativ starker linearer Zusammenhang} \\[6pt] 1 & = & \text{vollständiger Zusammenhang} \\ \end{array} \)
\(\\\)
Damit ist diese Verteilung der Erhebungswerte gut geeignet um stellvertretend als Gerade dargestellt zu werden.
\(\\[1em]\)