Polynomdivision
Inhaltsverzeichnis
\(\\\)
Beispiel einer Polynomdivision
Gegeben ist folgende Funktion:
\( \quad f(x) = x^3 - 4x^2 - 11x + 30 \)
\(\\\)
Für die Nullstellenberechnung gilt:
\( \quad 0 = x^3 - 4x^2 - 11x + 30 \)
\(\\\)
Wir stellen fest, dass sich hier weder das Ausklammern noch die Substitution anwenden lässt. Ist mindestens eine der Nullstellen ein ganzzahliger Wert, so können die Nullstellen mithilfe der Polynomdivision berechnet werden.
\(\\[2em]\)
Startwert der Polynomdivision
Dazu wird folgendermaßen vorgegangen: Wir spalten einen Linearfaktor von dem Funktionsterm ab, indem wir eine Nullstelle als Startwert nehmen. Diesen Startwert können wir auf zweierlei Arten ermitteln.
\(\\[1em]\)
Startwert über Probieren ermitteln
Meist ist eine Nullstellen ein ganzzahliger Teiler von der letzten Zahl des Funktionsterms, hier also von der 30. Das heißt, dass eine Nullstelle ein Element aus der Menge
\(\quad \{-30, -15, -10, -6, -3, -2, -1, 1, 2, 3, 6, 10, 15, 30 \} \)
\(\\\)
ist. Wir probieren zunächst die kleinsten Werte durch und arbeiten uns dann weiter hoch.
\( \quad \begin{array}{ r c l } f(1) & = & 1^3 - 4 \cdot 1^2 - 11 \cdot 1 + 30 \\[6pt] f(1) & = & 16 \\[20pt] f(-1) & = & (-1)^3 - 4 \cdot (-1)^2 - 11 \cdot (-1) + 30 \\[6pt] (-1) & = & 38 \\[20pt] f(2) & = & 2^3 - 4 \cdot 2^2 - 11 \cdot 2 + 30 \\[6pt] f(2) & = & \color{blue}{0} \\ \end{array} \)
\(\\[2em]\)
Startwert mit Wertetabelle bestimmen
Auf Taschenrechner CASIO fx-991DE X finden wir die Wertetabelle unter \(\boxed{MENU}\) \(\boxed{9}\). Zunächst geben wir die Funktion ein

\(\\\)
und bestätigen mit \(\boxed{=}\). Die 2. Funktion überspringen wir mit erneutem \(\boxed{=}\). Wir nehmen folgende Einstellungen vor:

\(\\\)
Die vollständigen Tabelle sieht folgendermaßen aus:
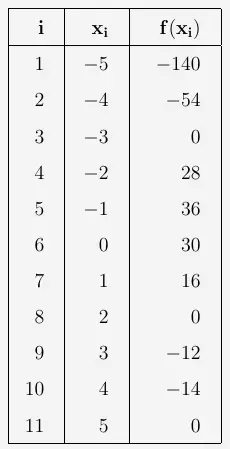
\(\\[2em]\)
Polynomdivision ausführen
Es wird der Linearfaktor \((x - 2)\) vom Funktionsterm abgespalten, oder besser gesagt: ausgeklammert.
\( \quad \left(x^3 - 4x^2 - 11x + 30\right) : \left(x - 2\right) \)
\(\\\)
Wir beginnen damit, dass wir den 1. Teil des Funktionsterms durch den 1. Teil des Linearfaktors teilen.
\( \quad \left(\color{blue}{x^3} - 4x^2 - 11x + 30\right) : \left(\color{blue}{x} - 2\right) \)
\(\\\)
Das berechnen wir folgendermaßen:
\( \quad x^3 : x = \frac{\; x^3}{x} =\frac{x \cdot x \cdot x}{x} = \frac{\not{x} \cdot x \cdot x}{\not{x}} =x^2 \)
\(\\\)
Daraus folgt
\( \quad \left( x^3 - 4x^2 - 11x + 30\right) : ( x - 2) \; = \; \color{blue}{x^2} \)
\(\\\)
Als Nächstes wird zurück multipliziert. Das heißt, dass das Ergebnis mit dem Linearfaktor ausmultipliziert wird.
\( \quad (x - 2) \cdot x^2 = x^3 - 2x^2 \)
\(\\\)
Das Ganze wird unter den Funktionsterm geschrieben.

\(\\\)
Dieser neue Ausdruck soll von dem Funktionsterm subtrahiert werden. Es wird eine Klammer um den Ausdruck gesetzt und ein Minuszeichen vor der Klammer platziert.

\(\\\)
Nun kommt ein Strich unter dem Ganzen.

\(\\\)
Die Klammer mit dem Minus davor wird aufgelöst.

\(\\\)
Die übereinander stehende Teile werden zusammen addiert und unter dem Strich geschrieben.

\(\\\)
Der nächste Teil des Funktionsterms wird nach unten gezogen.

\(\\\)
Ein Durchlauf ist geschafft. Nun wiederholt sich das Ganze. Wir können leicht erkennen, das im Grunde wie bei einer schriftlichen Division gearbeitet wird. Und genau das ist es ja auch, nur mit Polynomen.
Wir nehmen nun den 1. Teil vom neu gewonnenen Term und teilen ihn wieder durch den 1. Teil des Linearfaktors nach dem dem gleichen Prinzip wie zu Beginn.
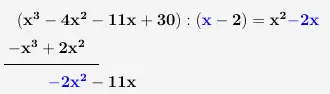
\(\\\)
Jetzt wird wieder zurück multipliziert, siehe 1. Durchlauf, und das Ergebnis mit einer Klammer versehen und ein Minus davor gesetzt.
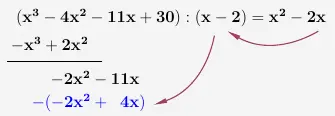
\(\\\)
Nun wird wieder ein Strich unter dem Ganzen gesetzt.
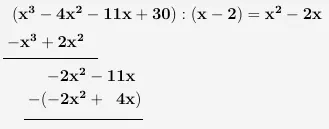
\(\\\)
Jetzt addieren wir die übereinander stehenden Teile, wobei wir, dieses Mal gedanklich, die Klammer schon aufgelöst haben. Das entspricht dann auch der richtigen Notation. Vorher habe ich es nur dem Verständnis halber ausführlicher dargestellt. Vorsicht mit den Vorzeichen. Bei Unsicherheiten einfach noch einmal den 1. Durchlauf durchgehen.

\(\\\)
Die letzte Stelle des Funktionsterms wird nun hinunter gezogen.
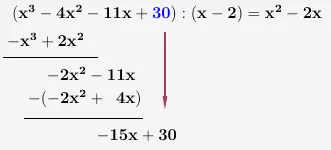
\(\\\)
Abermals teilen wir den 1. Teil des neuen Terms durch den 1. Teil des Linearfaktors.

\(\\\)
Ein letztes Mal multiplizieren wir zurück, Strich drunten und unter der Berücksichtigung des Klammerauflösens die übereinander stehenden Teile addieren.

Es ist kein Rest vorhanden.
\(\\[2em]\)
weitere Nullstellen bestimmen
Es gilt ja nun
\( \quad 0 = x^3 - 4x^2 - 11x + 30 \)
\(\\\)
also auch
\( \quad 0 = \left( x- 2\right) \cdot \left(x^2 - 2x -15\right) \)
\(\\\)
Die Nullstelle \(x=2\) kennen wir bereits. Weitere Nullstellen werden mit
\( \quad 0 = x^2 - 2x -15 \)
\(\\\)
berechnet, was wir mit der PQ-Formel lösen.
\( \quad \begin{array}{ r c l l } x_{2,3} & = -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q} \\[8pt] x_{2,3} & = -\frac{-2}{2}\pm \sqrt{\left(\frac{-2}{2}\right)^2-(-15)} \\[8pt] x_{2,3} & = 1 \pm \sqrt{(-1)^2 + 15} \\[6pt] x_{2,3} & = 1 \pm \sqrt{16} \\[6pt] x_{2,3} & = 1\pm 4 \\[6pt] x_2 & = 5 \\[6pt] x_3 & = -3 \\ \end{array} \)
\(\\\)
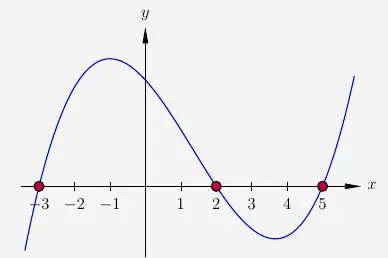
\(\\[1em]\)