Normalverteilung
Inhaltsverzeichnis
\(\\\)
Lagemaße bei Verteilungen
Bei Verteilungen spielen die beiden Lagemaße
- Erwartungswert \(\mu\)
- Standardabweichung \(\sigma\)
eine besondere Rolle. Betrachtet wird nun die Binomialverteilung mit
\( \begin{array}{ r c l } n & = & 100 \\ p & = & 0{,}7 \\ \end{array} \)
\(\\\)
Das Histogramm davon ist für \(53 \leq x \leq 87\) dargestellt.
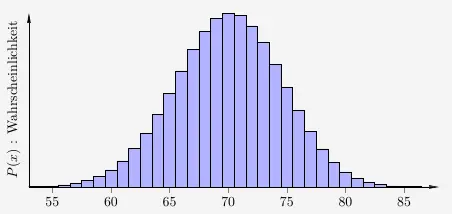
Die dazugehörigen Lagemaße sind
\( \begin{array}{ r c c c c c l } \mu & = & n \cdot p & = & 100 \cdot 0{,}7 & = & 70 \\ \end{array} \)
\(\\\)
und
\( \begin{array}{ r c c c c c l } \sigma & = & \sqrt{n \cdot p \cdot (1-p)} & = & \sqrt{100 \cdot 0{,}7 \cdot (1-0{,}7)} & = & 4{,}58 \\ \end{array} \)
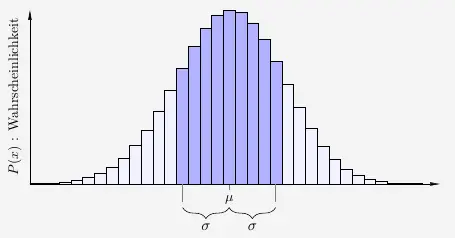
Der Erwartungswert ist der Durchschnittswert der Verteilung und zugleich der \(x\)-Wert mit der größten Wahrscheinlichkeit.
Die Standardabweichung ist die durchschnittliche Abweichung der Verteilung vom Erwartungswert. Sie ist eine Maß für die Streuung um den Erwartungswert.
\(\\[2em]\)
Eigenschaften der Normalverteilung
Die Binomialverteilung kann näherungsweise durch eine stetige Verteilung, die Normalverteilung,
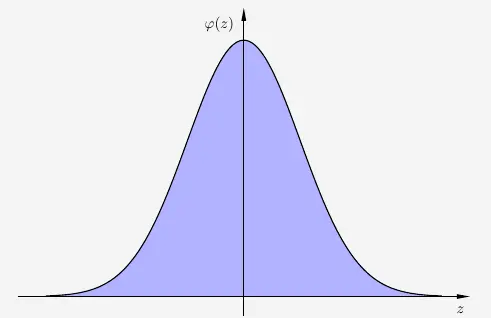
beschrieben werden. Die Normalverteilung ist der Graph der Funktion
\( \varphi(z) \, = \, \frac{1}{\sqrt{2 \pi}} \cdot e^{-\frac{1}{2}z^2} \)
\(\\\)
und stellt die Gauß'sche Glockenkurve dar. Die Normalverteilung hat einen besonderen Erwartungswert und eine besondere Standardabweichung mit
\( \begin{array}{ r c l } \mu & = & 0 \\ \sigma & = & 1 \\ \end{array} \)
\(\\\)
Deshalb ist es recht einfach, das \(k\) einer Binomialverteilung in den \(z\)-Wert der Normalverteilung umzurechnen.
\(\\[2em]\)
Anpassung der Binomialverteilung an die Normalverteilung
Um die Binomialverteilung näherungsweise durch die Normalverteilung auszudrücken, wird Binomialverteilung um den Erwartungswert nach links verschoben und in \(x\)-Richtung gestaucht.
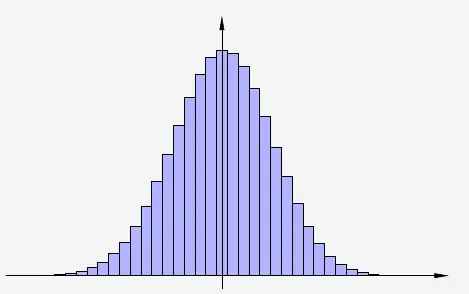
Dies geschieht mit der Umrechnung des \(k\)-Wertes
\( z \, = \, \frac{k - \mu}{\sigma} \)
in den \(z\)-Wert der Normalverteilung.
\(\\[2em]\)
Sigma-Umgebung
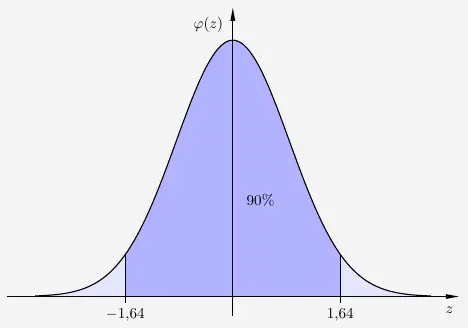
Jedem \(z\)-Wert der Normalverteilung ist nun eine bestimmte Wahrscheinlichkeit (Fläche unter dem Graphen) zugeordnet.
Lösen wir den Ausdruck
\( \begin{array}{ r c l } z & = & \frac{k - \mu}{\sigma} \\ \end{array} \)
\(\\\)
nach \(k\) auf mit
\( \begin{array}{ r c l l } z & = & \frac{k - \mu}{\sigma} & \bigl| \, \cdot \sigma \\ z \cdot \sigma & = & k - \mu & \bigl| \, + \mu \\ \mu + z \cdot \sigma & = & k \, , \\ \end{array} \)
\(\\\)
so ergibt sich die \(\sigma\)-Umgebung einer Binomialverteilung.
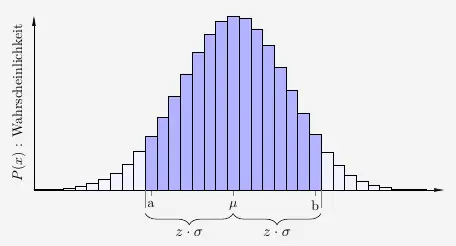
Der \(z\)-Wert wird als der Radius der \(\sigma\)-Umgebung bezeichnet und gibt den Abstand zum Erwartungswert bei der Normalverteilung an. Übliche Radien sind
\( \begin{array}{ | c | c | } \hline \text{Radius} & \sigma \text{-Umgebung} \\ \hline 1{,}64 & 90 \% \\ 1{,}96 & 95 \% \\ 2{,}58 & 99 \% \\ \hline \end{array} \)
\(\\[2em]\)
Wahrscheinlichkeit mit der Normalverteilung
Zu berechnen ist die Wahrscheinlichkeit der Binomialverteilung
\( P(x \leq 65) \)
\(\\\)
mit
\( \begin{array}{ r c l } n & = & 100 \\ p & = & 0{,}7 \\ \end{array} \)
\(\\\)
Die Berechnung mit der Normalverteilung erfolgt in \(2\) Schritten:
- Umwandlung des \(k\)-Wertes in den \(z\)-Wert
- Ermittlung der Wahrscheinlichkeit (Fläche unter dem Graphen)
\(\\[2em]\)
Umrechnung des k-Wertes der Binomialverteilung
Nach der bekannten Formel
\( z \, = \, \frac{k - \mu}{\sigma} \)
\(\\\)
ermitteln wir den \(z\)-Wert.
\( \begin{array}{ r c l } z & = & \frac{65 - 100 \cdot 0{,}7}{\sqrt{100 \cdot 0{,}7 \cdot (1-0{,}7)}} \\[6pt] z & = & -1{,}09 \\ \end{array} \)
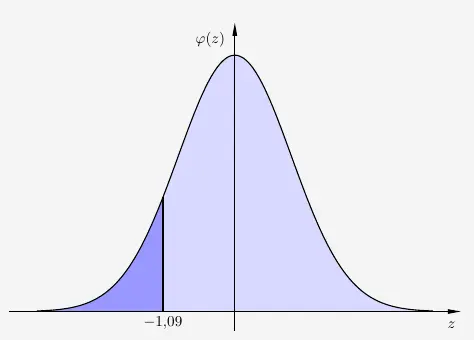
Per Integralrechnung mit
\( \begin{array}{ r c l c l } A & = & \displaystyle{\int}_a^b \varphi(z) dz & = & \Phi(b) - \Phi(a) \\[12pt] & = & \displaystyle{\int}_{\lim \limits_{z \to \infty}(a)}^{-1{,}09} \varphi(z) dz & = & 0 - \Phi(-1{,}09) \\[12pt] & = & \Phi(-1{,}09) \\ \end{array} \)
\(\\\)
kann die Wahrscheinlichkeit berechnet werden. Bevor wir jetzt dieses \(\Phi(z)\) bestimmen, müssen wir noch kontrollieren, ob \(z=-1{,}09\) wirklich der korrekte Wert für \(z\) ist. Denn bei der Umwandlung von einer diskreten Verteilung in eine steige Verteilung muss Folgendes berücksichtigt werden.
\(\\[1em]\)
Stetigkeitskorrektur
Betrachtet wir die beiden Verteilungen,
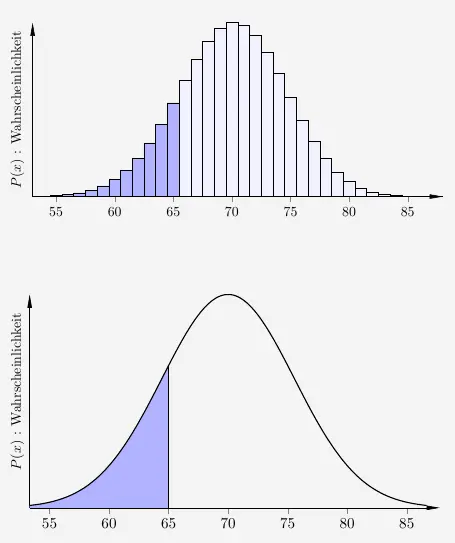
so ist zu erkennen, dass der rechte Rand der gesuchten Fläche in der Binomialverteilung weiter rechts als \(65\) liegt. Das liegt daran, dass in der Binomialverteilung der Wert für \(k=65\) von \(64{,}5\) bis \(65{,}5\) dargestellt ist. Damit wir in der Normalverteilung eine vergleichbare Fläche erhalten, muss in der Umrechnung der \(k\)-Wert mit der Stetigkeitskorrektur von \(0{,}5\) angepasst werden. Daraus folgt
\( \begin{array}{ r c l } z & = & \frac{k + 0{,}5 - \mu}{\sigma} \\[6pt] z & = & \frac{65 + 0{,}5 - 100 \cdot 0{,}7}{\sqrt{100 \cdot 0{,}7 \cdot (1-0{,}7)}} \\[6pt] z & = & -0{,}98 \\ \end{array} \)
\(\\\)
Die korrekte Bestimmung der gesuchten Wahrscheinlichkeit erfolgt also mit \(\Phi(-0{,}98)\). Diese kann
- aus einer geeigneten Tabelle abgelesen oder
- mit der entsprechenden Taschenrechnerfunktion bestimmt werden.
\(\\[1em]\)