Linksseitiger Signifikanztest
Inhaltsverzeichnis
\(\\\)
Aufgabenstellung
Ein Maschinenfabrikant hat sich auf die Herstellung von Hutmuttern, Ringmuttern und Flügelmuttern spezialisiert. Bei den Hutmuttern hat er bisher einen Ausschuss von \(8\%\) gehabt. Der Maschinenfabrikant vermutet nun, dass durch Einführung neuer Produktionsmaschinen sich der Ausschussanteil der Hutmuttern reduziert habe.
Es wird eine Stichprobe von \(500\) Hutmuttern untersucht, die mit den neuen Maschinen produziert wurden. Führe einen Signifikanztest durch, um diese Vermutung auf einem Signifikanzniveau von \(6\%\) zu stützen.
Verwende dabei die Näherung mit der Normalverteilung.
\(\\[2em]\)
Variablendeklaration
\(x\) beschreibt die Anzahl der Hutmuttern, die Ausschuss sind. \(x\) ist binomialverteilt mit \(n=500\).
\(\\[2em]\)
Hypothesen formulieren
Die Vermutung \(p < 0{,}08\) ist nachzuweisen. Wie kann das nun erreicht werden?
Der Maschinenfabrikant vermutet, dass der Ausschuss weniger als \(8\%\) ist. Wie viel Prozent es sind, kann er jedoch nicht sagen. Dagegen wissen wir, dass bisher der Ausschuss \(8\%\) war. Davon können wir auf der Basis des Signifikanzniveaus den Annahme- und Verwerfungsbereich bestimmen. Wir wählen in Übereinstimmung mit dem Prinzip des Hypothesentests diese Hypothese als Nullhypothese mit
\( \quad \begin{array}{ r l } h_0: & p = 0{,}08 \\ \end{array} \)
Wie beim Alternativtest arbeiten wir mit zwei sich gegenseitig ausschließende Hypothesen. Die Vermutung ist die \(h_1\)-Hypothese. Da die eine Hypothese die Gegenhypothese der jeweils anderen ist, können wir die Nullhypothese noch schärfer formulieren und kommen zu den Hypothesen
\( \quad \begin{array}{ r l } h_0: & p \geq 0{,}08 \\[5pt] h_1: & p < 0{,}08 \\ \end{array} \)
\(\\[1em]\)
Merke:
-
Wähle die Vermutung als die \(h_1\)-Hypothese.
-
Die Gegenhypothese dazu ist die Nullhypothese. Die Nullhypothese enthält ,,p ist gleich \(\dots\)‘’
-
Die Nullhypothese ist unsere Arbeitshypothese.
\(\\[2em]\)
Verwerfungsbereich der Nullhypothese berechnen
Das die eine Hypothese das Gegenteil der anderen ist, zeigt sich nicht nur beim \(p\)-Wert, sondern auch bei den Annahme- und Verwerfungsbereichen. Diese sind für die Nullhypothese
\( \quad \begin{array}{ r c l } V & = & \{ 0 \, , \, \cdots \, , \, k \} \\ A & = & \{ k+1 \, , \, \cdots \, , \, 500 \} \\ \end{array} \)
\(\\\)
und für die \(h_1\)-Hypothese ist der Annahme- und Verwerfungsbereich
\( \quad \begin{array}{ r c l } A & = & \{ 0 \, , \, \cdots \, , \, k \} \\[5pt] V & = & \{ k+1 \, , \, \cdots \, , \, 500 \} \\ \end{array} \)
\(\\\)
Graphisch veranschaulicht:
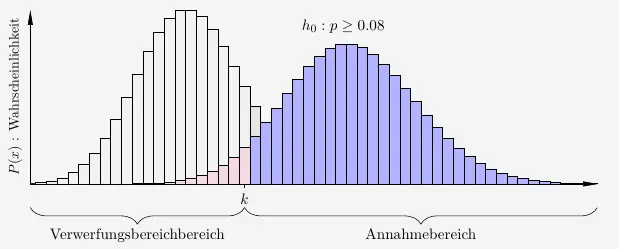
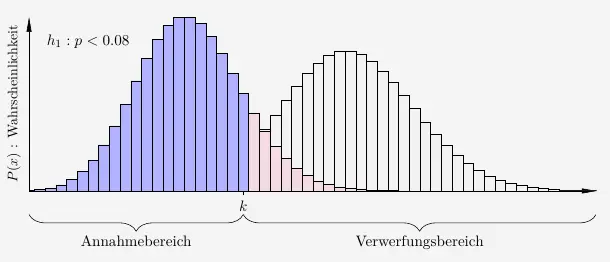
Um den Annahmebereich der Vermutung \(h_1\) zu berechnen, ermitteln wir einfach den Verwerfungsbereich der Nullhypothese. Beide haben das Intervall \([0;k]\). Denn der Verwerfungsbereich der Nullhypothese ist ja mit \(\alpha=6\%\) vorgegeben.
\(\\[2em]\)
Stelle k ermitteln
Die Stelle \(k\) wird durch die Näherung mit der Normalverteilung ermittelt.
\(\\\)
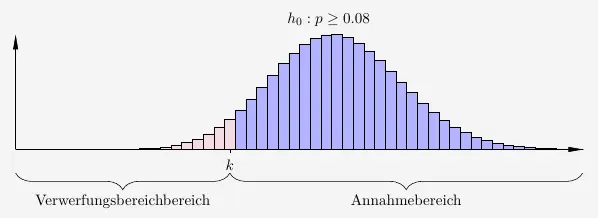
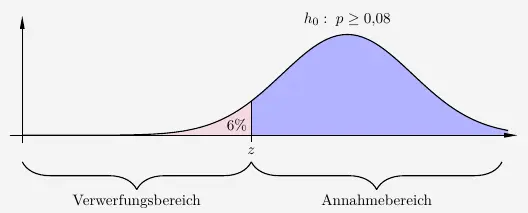
\(\\\)
Für den Verwerungsbereich gilt
\( \quad P(x \leq k) \, = \, \Phi(z) \)
\(\\\)
Mit der Stetigkeitskorrektur ist
\( \quad z \, = \, \frac{k + 0{,}5 - \mu}{\sigma} \)
\(\\\)
Aufgrund der Signikanz von \(\alpha \, = \, 6\%\) gilt weiter
\( \quad \begin{array}{ r c l } P(x \leq k) & \leq & 0{,}06 \\[5pt] \Phi(\frac{k + 0{,}5 - \mu}{\sigma}) & \leq & 0{,}06 \\ \end{array}\)
\(\\\)
Um \(k\) aus \(\Phi(z)\) zu ermitteln benötigen wir den Erwartungswert mit
\( \quad \begin{array}{ r c c c l } \mu & = & 500 \cdot 0{,}08 & = & 40 \\ \end{array} \)
\(\\\)
und die Standardabweichung mit
\( \quad \begin{array}{ r c c c c c l } \sigma & = & \sqrt{n \cdot p \cdot (1-p)} & = & \sqrt{500 \cdot 0{,}08 \cdot (1-0{,}08)} & = & 6{,}07 \\ \end{array} \)
\(\\\)
Die Stelle \(k\) kann auf zwei Arten mit der Normalverteilung bestimmt werden, durch
\(\\[1em]\)
Berechnung mit dem Taschenrechner
Der einfachste Weg ist sicherlich mit der inversen Normalverteilung mithilfe des Taschenrechners.
Es ergibt sich \(k\) mit
\( \quad \begin{array}{ r c l l } k + 0{,}5 & = & \Phi_{\mu \, ; \, \sigma}^{-1}(\alpha) \\[6pt] k + 0{,}5 & = & \Phi_{40 \, ; \, 6{,}07}^{-1}(0{,}06) \\[5pt] k + 0{,}5 & = & 30{,}56 & | \, -0{,}5 \\[4pt] k & = & 30{,}06 \\ \end{array} \)
\(\\\)
Wir erhalten \(k=30\).
\(\\[1em]\)
Berechnung mit der Tabelle
Aus der Tabelle lässt sich der Wert
\( \quad z \, = \, -1{,}55 \)
\(\\\)
ablesen. Es gilt nun
\( \quad \begin{array}{ r c l l } \frac{k + 0{,}5 - \mu}{\sigma} & = & z & | \, \cdot \sigma \\[6pt] k + 0{,}5 - \mu & = & z \cdot \sigma & | \,+ \mu \\[5pt] k + 0{,}5 & = & \mu + z \cdot \sigma & | \,- 0{,}5 \\[5pt] k & = & \mu + z \cdot \sigma - 0{,}5 \\[4pt] k & = & 40 - 1{,}55 \cdot 6{,}07 - 0{,}5 \\[4pt] k & = & 30{,}09 \\ \end{array} \)
\(\\\)
Wir erhalten \(k=30\).
\(\\[2em]\)
Entscheidungsregel aufstellen
Es folgt der Verwerfungs-und Annahmebereich der Nullhypothese.
\( \quad \begin{array}{ r c l } V & = & \{ 0 \, , \, \cdots \, , \, 30 \} \\[5pt] A & = & \{ 31 \, , \, \cdots \, , \, 500 \} \\ \end{array} \)
\(\\\)
Der Verwerfungsbereich der Nullhypothese ist gleichzeitig der Annahmebereich der \(h_1\)-Hypothese. Damit ist die
\(\\\) Entscheidungsregel:
Haben wir bei der Stichprobe von \(500\) Hutmuttern höchstens eine Ausschussquote von \(30\) Stück, so kann die Vermutung des Maschinenfabrikanten, dass mit der Einführung neuer Maschinen sich der Anteil an Ausschuss bei Hutmuttern reduziert habe, gestützt werden.
\(\\[2em]\)
Fehler 2. Art
Tatsächlich haben die neuen Maschinen eine Ausschussquote von \(5\%\) Wie lautet der \(\beta\)-Fehler?
An der gleichen Grenze \(k\) wird der Verwerfungsbereich von \(h_1\) berechnet.
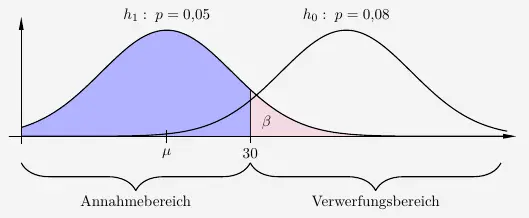
\( \quad \begin{array}{ r c l } \beta & = & P_{500 \, ; \, 0{,}05}(x > 30) \\[5pt] & = & 1 - P_{500 \, ; \, 0{,}05}(x \leq 30) \\[5pt] & = & 1 - 0{,}8692 \\[5pt] & = & 0{,}1308 \\[5pt] & = & 13{,}08 \% \\ \end{array} \)
\(\\[2em]\)