Vektoren
Inhaltsverzeichnis
\(\\\)
1. Vektoren und Skalare
In der Vektorrechnung haben wir es mit Vektoren und Skalaren zu tun. Um den Unterschied deutlich zu machen, dient ein Stein auf der Erdoberfläche als Anschauungsobjekt.
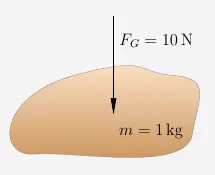
Die Masse des Steins von 1 kg ist ein Skalar und hat deshalb nur eine Größe.
Die Gewichtskraft von 10 Newton ist ein Vektor und hat ein Größe und eine Richtung, die zum Erdmittelpunkt hin zeigt.
\(\\[2em]\)
2. Ortsvektor
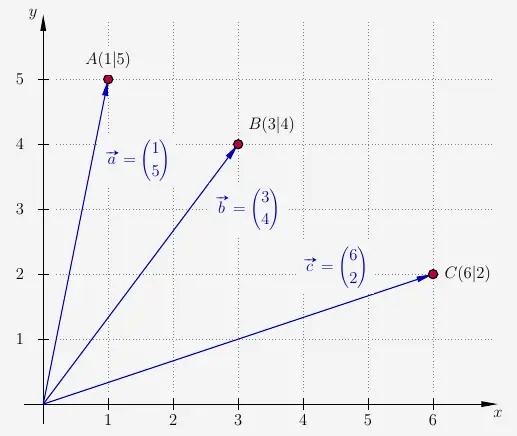
Ortsvektoren laufen stets vom Koordinatenursprung \(O\) (lateinisch Origo : „Ursprung’‘) zu dem Punkt, der zu dem Ortsvektor gehört, hier Punkt \(A\), \(B\) oder \(C\), und werden geschrieben als \(\vec{OA}\), \(\vec{OB}\) oder \(\vec{OC}\). Sie können auch einfach kurz wie in diesem Beispiel als \(\vec{a}\), \(\vec{b}\) oder \(\vec{c}\) bezeichnet werden.
Ortsvektoren haben die gleichen Werte wie die Koordinaten des Punktes.
\(\\[2em]\)
3. Vektor und Gegenvektor
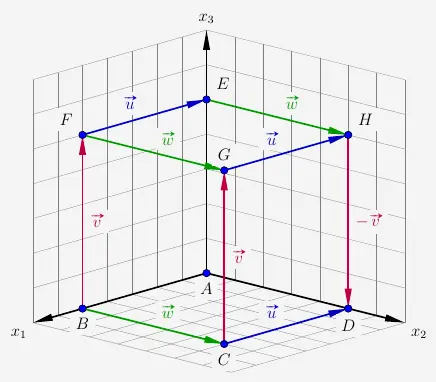
Im Gegensatz zu Punkten, die durch ihre Koordinaten eindeutig positioniert sind, haben Vektoren keine festgelegte Position und können an beliebigen Orten vorhanden sein. Gleiche Vektoren sind dadurch gekennzeichnet, dass sie parallel zueinander sind, die gleiche Länge haben und in die gleiche Richtung verlaufen.
Ein Vektor, der parallel zu einem anderen Vektor ist und die gleiche Länge hat, jedoch in die entgegen gesetzte Richtung verläuft, heißt Gegenvektor. In der obigen Darstellung ist der Vektor \(\vec{HD}\) Gegenvektor zu \(\vec{v}\) und wird als -\(\vec{v}\) geschrieben.
\(\\[2em]\)
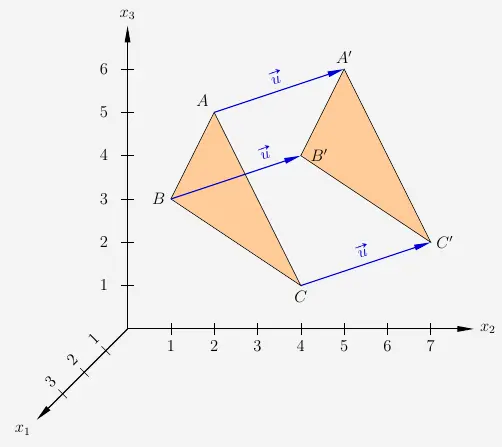
4. Vektoren als Bewegung
Vektoren können beispielsweise eine Bewegung sein. Hier drückt der Vektor \(\vec{u}\) die Verschiebung des Dreiecks \(ABC\) zu der neuen Position \(A'B'C'\) aus.
\(\\[2em]\)
5. Verbindungsvektor
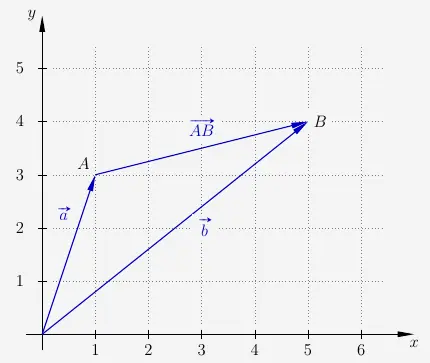
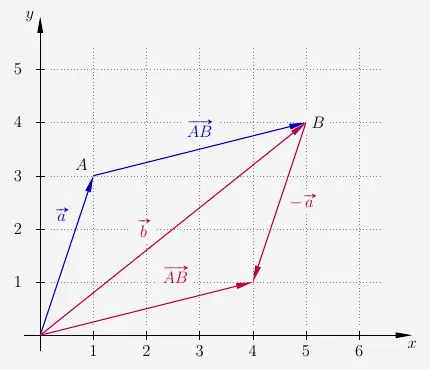
Mit der Vektoraddition
\(\quad \vec{a} + \vec{AB} \)
erreichen wir den Punkt \(B\) ebenso wie mit dem Vektor \(\vec{b}\). Es gilt also
\(\quad \begin{array}{ r c l } \vec{a} + \vec{AB} & = & \vec{b} \\ \end{array} \)
Durch Umformen der Gleichung erhalten wir den Verbindungsvektor von \(A\) und \(B\).
\(\quad \begin{array}{ r c l l } \vec{a} + \vec{AB} & = & \vec{b} & | \, - \vec{a} \\[5pt] \vec{AB} & = & \vec{b} - \vec{a} \\ \end{array} \)
Merke:
Der Verbindungsvektor zweier Punkte ist stets die Rechnung
,,Ortsvektor des Zielpunktes’‘ – ,,Ortsvektor des Startpunktes’‘
Graphisch lässt sich nun auch anders zeigen, das \(\vec{b} - \vec{a}\) den Vektor \(\vec{AB}\) ergibt. Der Vektor \(-\vec{a}\) ist der Gegenvektor von \(\vec{a}\). Es gilt dann
\(\quad \vec{b} - \vec{a} = \vec{b} + \left(-\vec{a}\right) \)
Wir haben also eine Vektorkette von \(\vec{b}\) und \(-\vec{a}\). Das stellt sich folgendermaßen dar: