Potenzfunktionen mit negativen Exponenten
Inhaltsverzeichnis
\(\\\)
Negative Exponenten
Bei Funktionstermen von der Art
\( \quad x^{-1} \, {,} \; x^{-2} \, {,} \; x^{-3} \, {,} \; x^{-4} \, {,} \; \dots \)
\(\\\)
ist es unüblich, sie in dieser Art mit negativen Exponenten zu notieren. Vielmehr werden die Terme mithilfe der Potenzregel
\( \quad \boxed{x^{-n} \; = \; \frac{1}{x^n}} \)
\(\\\)
umgeschrieben. Es geben sich dann die Terme
\( \quad \frac{1}{x} \, {,} \; \frac{1}{x^2} \, {,} \; \frac{1}{x^3} \, {,} \; \frac{1}{x^4} \, {,} \; \dots \)
\(\\\)
Ebenso wie bei den Potenzfunktionen mit positiven Exponenten ergeben sich auch hier vier Darstellungsformen. In jeder Gruppe sind die Graphen recht ähnlich. Deshalb ist hier aus jeder Gruppe der besseren Übersicht halber nur ein Graph gezeichnet.
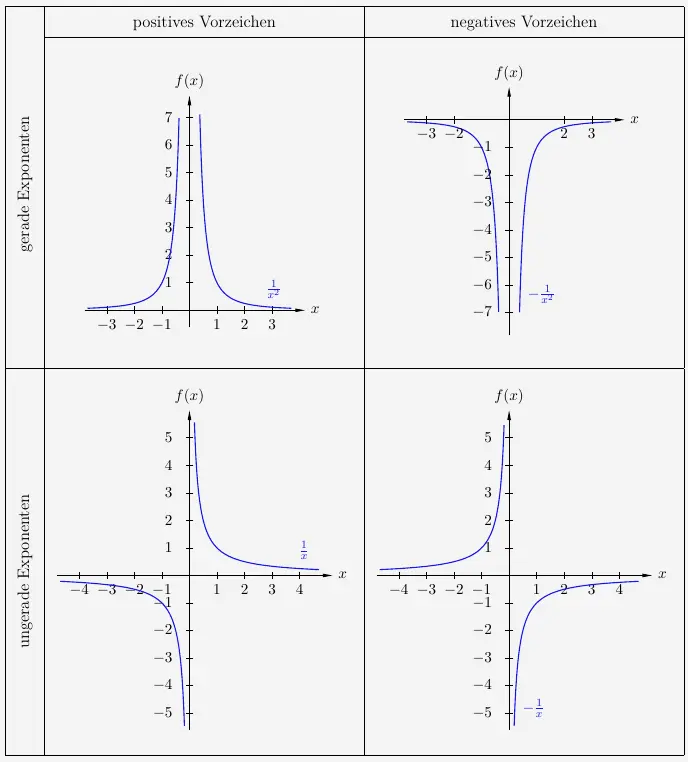
\(\\[2em]\)
Polstellen bei Potenzfunktionen
Wie man es nach den Zeichnungen erahnt, kommen die Funktionen an der Stelle \(x=0\) nicht vor. Das ist auch leicht einsehbar, denn wenn man für \(x\) Null einsetzt erhält man bei jeder dieser Funktion
\( \quad \frac{1}{0} \)
\(\\\)
Durch Null teilen ist nicht definiert. Solche Art von Definitionslücken bei einer Stelle \(x\) heißen Pole oder Polstellen. Bei allen dargestellten Funktionen ergibt sich deshalb der Definitionsbereich
\( \quad \mathbb{D} \; = \; \mathbb{R}\setminus{\{0\}} \)
\(\\[1em]\)
Grenzwertverhalten bei Potenzfunktionen
Randverhalten
Für die oben dargestellten und damit auch für alle Potenzfunktionen mit negativen Exponenten ergibt sich
\( \quad \lim \limits_{x \to \pm \infty} f(x) = 0 \)
\(\\[1em]\)
Verhalten für × strebt gegen Null bei Potenzfunktionen
Betrachten wir die Grenzwerte an einer Polstelle, so müssen wir die linkseitigen und rechtsseitigen Grenzwerte bestimmen.
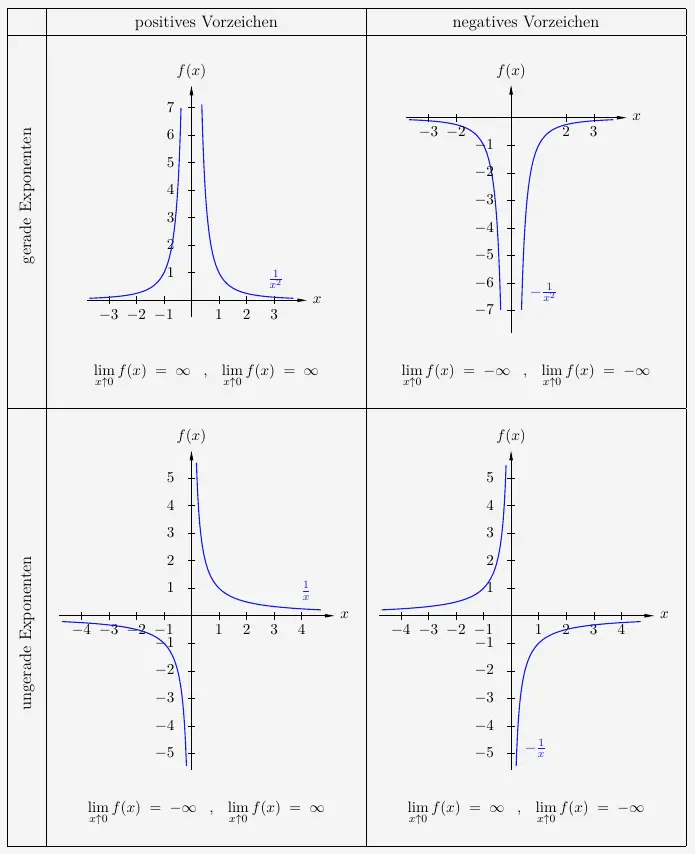
\(\\[2em]\)
Symmetrie
Die Symmetrie ist ebenso wie bei den Potenzfunktionen mit positiven Exponenten. Auch hier gilt, dass Potenzfunktionen mit
-
geraden Exponenten eine Achsensymmetrie aufweisen.
-
ungeraden Exponenten eine Punktsymmetrie aufweisen.
\(\\[2em]\)
Übersicht Potenzfunktionen mit negativen Exponenten
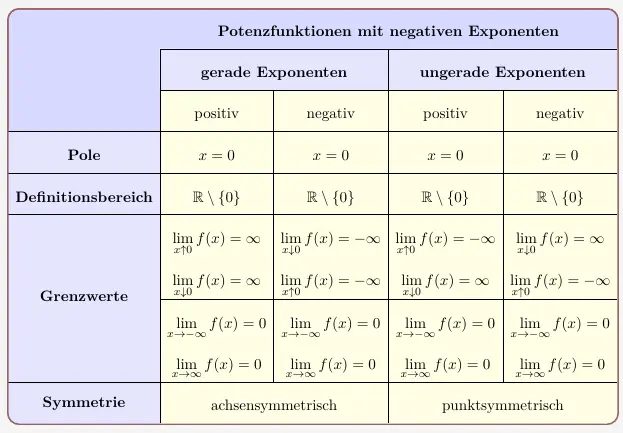
\(\\[1em]\)