Aufgaben

---

\(\\\)

“Streckenzug”

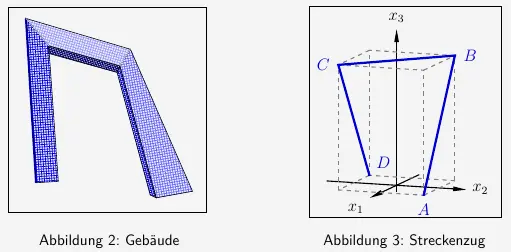
Im Koordinatensystem ist der Streckenzug abgebildet, der aus den Strecken \(\overline{AB}\), \(\overline{BC}\) und \(\overline{CD}\) besteht mit

\( \quad A(11|11|0)\), \(B(-11|11|28)\), \(C(11|-11|28)\) und \(D(-11|-11|0) \).

\(\\\)

Die Punkte \(A\), \(B\), \(C\) und \(D\) sind Eckpunkte eines Quaders, der gestrichelt dargestellt ist.

\(\qquad \quad\) Arbeitsblatt ausdrucken

\(\\[1em]\)

Abbildung

1. Zeichnen Sie den Mittelpunkt \(M\) der Strecke \(\overline{AB}\) in die obige Abbildung und geben Sie seine Koordinaten an.

   (2 P)

\(\\\)

2. Prüfen Sie rechnerisch, ob der Punkt \(N(-9|-11|3)\) auf der Strecke\(\overline{CD}\) liegt.

   (5 P)

\(\\\)

3. Berechnen Sie die Länge des abgebildeten Streckenzuges.

   (3 P)

Lösung

\(\\[2em]\)

Ebene E

Die Ebene \(E\) enthält die Punkte \(A\), \(B\) und \(C\).

\(\\\)

1. Bestimmen Sie eine Gleichung von \(E\) in Koordinatenform.

   \( \qquad \big[\textrm{Kontrolle:} \quad 14 x_1 + 14 x_2 + 11 x_3 = 308 \big] \)

   (4 P)

\(\\\)

2. Der Abstand des Punktes \(D\) von der Ebene \(E\) wird mit \(d\) bezeichnet.

   • Berechnen Sie den Wert von \(d\).

   • Begründen Sie, dass der Term \(\frac{d}{6} \cdot \bigl|\overrightarrow{AB} \times \overrightarrow{BC}\bigl|\) das Volumen der Pyramide \(ABCD\) angibt.

     (6 P)

\(\\\)

3. Berechnen Sie die Größe des Winkels \(\varphi\), unter dem \(E\) die \(x_1x_2\)-Ebene schneidet.

   (4 P)

Lösung

\(\\[2em]\)

Reelle Zahl h

Für jede reelle Zahl \(h\) wird der Punkt \(P_h(0|0|h)\) betrachtet.

\(\\\)

1. Beschreiben Sie die Lage des Punktes \(P_h\) für \(0<h<28\).

   (2 P)

\(\\\)

2. Bestimmen Sie die beiden Werte von \(h\), so dass ein Dreieck \(BP_hC\) mit rechtem Winkel bei \(P_h\) vorliegt, und geben Sie alle Werte von \(h\) an, für die sich ein stumpfwinkliges Dreieck \(BP_hC\) ergibt.

   (6 P)

\(\\\)

3. Im Folgenden liegt der Punkt \(P_h\) innerhalb des Quaders und hat von den drei Strecken \(\overline{AB}\), \(\overline{BC}\) und \(\overline{CD}\) den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von \(h\):

\( \qquad \begin{array}{ r l } \textrm{I.} & \overrightarrow{OQ} \; = \; \begin{smallmatrix} \left( \begin{array}{r} 11 \\ 11 \\ 0 \end{array} \right) \end{smallmatrix} +t \cdot \begin{smallmatrix} \left( \begin{array}{r} -22 \\ 0 \\ 28 \end{array} \right) \end{smallmatrix} \; , \; t \in [0;1] \\[8pt] \textrm{II.} & \overrightarrow{P_hQ} \circ \overrightarrow{AB} \; = \; 0 \\[8pt] \textrm{III.} & \bigl| \overrightarrow{P_hQ}\bigl| \; = \; 28 - h \\ \end{array} \)

\(\\\)

Erläutern Sie die Überlegungen, die diesem Vorgehen zur Bestimmung des Wertes von \(h\) zugrunde liegen.

(4 P)

Lösung

\(\\[2em]\)

Blickrichtungen

Der Streckenzug wird schließlich zur Modellierung des abgebildeten Gebäudes verwendet.

Das Gebäude wird mit verschiedene Blickrichtungen betrachtet.

\(\\\)

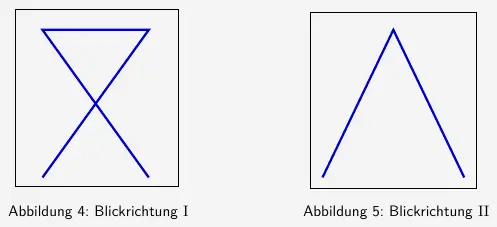
1. Die folgende Abbildungen stellen das Gebäude für zwei Blickrichtungen schematisch dar.

Geben Sie zu jeder der beiden Abbildungen einen möglichen Vektor an, der die zugehörige Blickrichtung beschreibt.

(2 P)

\(\\\)

2. Stellen Sie das Gebäude schematisch für eine Betrachtung von oben dar.

   (2 P)

Lösung

\(\\[2em]\)