HMF 3 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Graph einzeichnen
Nach den Voraussetzungen haben wir einen Punkt bei \((0|2)\) und einen Hochpunkt bei \(x=-1\). Wir können zum Beispiel den Hochpunkt \(H(-1|3)\) nehmen.
Der einfachste Graph wäre wohl eine nach unten geöffnete Parabel.
\(\\\)
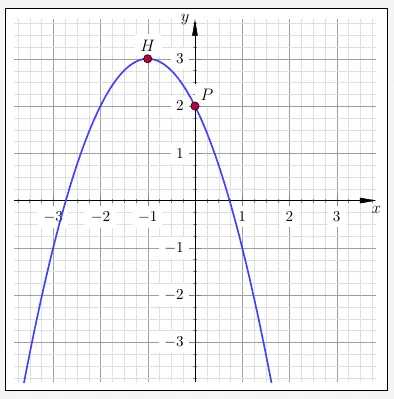
\(\\[2em]\)
Aufgabe 2 – Wert b und c
Bei der 2. Ableitung haben wir keine konkrete Zuweisung eines Werte, bei der 1. Ableitung allerdings schon. Wir arbeiten also mit
\( \quad \begin{array}{ r c l } f(x) & = & -0{,}5x^3 + bx + c \\[6pt] f'(x) & = & -1{,}5x^2 + b \\ \end{array} \)
\(\\\)
Es gilt
\( \quad \begin{array}{ r c l } \textrm{I} & f(0) & = & 2 \\[6pt] \textrm{II} & f'(-1) & = & 0 \\ \end{array} \)
\(\\\)
Diese Bedingungen in die oberen Gleichungen eingesetzt ergibt
\( \quad \begin{array}{ r c l } \textrm{I} & 2 & = & -0{,}5 \cdot 0^3 + b \cdot 0 + c \\[6pt] \textrm{II} & 0 & = & -1{,}5 \cdot (-1)^2 + b \\[20pt] \textrm{I} & 2 & = & c \\[6pt] \textrm{II} & 0 & = & -1{,}5 + b & | + 1{,}5 \\[20pt] \textrm{I} & 2 & = & c \\[6pt] \textrm{II} & 1{,}5 & = & b \\ \end{array} \)
\(\\\)