Winkel und Normale
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Winkel
Der eingeschlossene Winkel der beiden Tangenten wird mithilfe der Tangentensteigungen berechnet. Es gilt
\( \quad tan (\alpha) \; = \; m \)
\(\\\)
Zunächst bestimmen wir die Steigungen \(m\) der beiden Funktionen \(l\) und \(f\) an der Stelle \(x=0\). Das heißt, dass
\( \quad m_l \; = l'(0) \quad \textit{und} \quad m_f \; = f'(0) \)
\(\\\)
ist.

\(\\\)
Die zu den Steigungen gehörenden Steigungswinkel berechnen wir mit der Arkusfunktion des Tangens. Diese Arkusfunktion finden wir auf dem CAS unter der Taste \(\boxed{Trig}\) :
 \(\\\)
\(\\\)
Wir berechnen die Winkel mit

\(\\\)
Auf der Abbildung ist leicht zu erkennen,
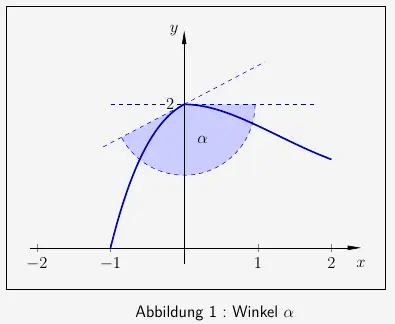
\(\\\)
dass der eingeschlossene Winkel \(\alpha\) nicht \(28{,}369^{\circ}\) sein kann. Deshalb schauen wir uns nun die Winkeleinteilung mit dem zugehörigen Tangens im Einheitskreis an. Demzufolge gilt
\( \quad tan(\beta) \; = \; tan(\beta + 180^{\circ}) \)
\(\\\)
und
\( \quad tan(\gamma) \; = \; tan(\gamma + 360^{\circ}) \)
\(\\\)
Damit erhalten wir
\( \quad \beta \; = \; 28{,}369^{\circ} + 180^{\circ} \; = \; 208{,}369^{\circ} \)
\(\\\)
und
\( \quad \gamma \; = \; 0^{\circ} + 360^{\circ} \; = \; 360^{\circ} \)
\(\\\)
Für den eingeschlossenen Winkel \(\alpha\) gilt nun
\( \quad \alpha \; = \; \gamma - \beta \; = \; 360^{\circ} - 208{,}369^{\circ} \; = \; 151{,}631^{\circ} \)
\(\\[2em]\)
Aufgabe 2 – Normale an Funktion l im Punkt P
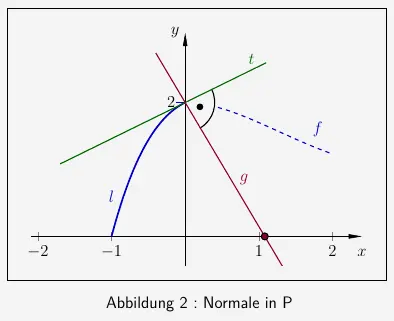
\(\\\)
Wie hier zu sehen ist, verläuft die Gerade \(g\) mit
\( \quad g(x) \; = \; m \cdot x +b \)
\(\\\)
rechtwinklig zur Tangente \(t\) durch den Punkt \(P( 0|2 )\). Diese Gerade nennt man die Normale von dem Graphen \(l\) an dem Punkt \(P\).
\(b\) ist der Achsenabschnitt und ist
\( \quad g(0) \; = \; 2 \)
\(\\\)
Die Steigung wird über die Steigung der Tangente bestimmt. Es gilt
\( \quad m_g \; = \; -\frac{1}{m_t} \; = \; -\frac{1}{0{,}54} \; = \; -\frac{50}{27} \)
\(\\\)
Damit ist
\( \quad g(x) \; = \; -\frac{50}{27} x + 2 \)
\(\\\)
Um den Schnittpunkt mit der \(x\)-Achse zu bestimmen berechnen wir die Nullstelle von \(g\) mit \(g(x)=0\).

Die \(x\)-Achse wird also bei \(N( 1{,}08 | 0 )\) geschnitten.
\(\\\)