Varianz und Standardabweichung mit dem Casio fx-991DE X
Die Varianz und Standardabweichung sowie weitere Werte einer Häufigkeitstabelle können mit der Funktion Statistik angezeigt werden.
\(\\\)
Dafür muss die entsprechende Tabelle so eingestellt werden, dass die Häufigkeiten von \(x\)-Werten eingegeben werden können.
Wir gehen dazu in das SETUP-Menu mit \(\boxed{\color{#C19A6B}{SHIFT}}\) \(\boxed{MENU}\)

\(\\\)
Mit

\(\\\)
bekommen wir

\(\\\)
\(\boxed{3}\) auswählen

\(\\\)
und \(\boxed{1}\) auswählen. Jetzt ist diese Einstellung gespeichert. Wenn man öfter mit den Häufigkeitstabellen arbeitet, kann man das so stehen lassen und braucht nicht immer wieder diese Einstellung vornehmen. Ansonsten können wir nach Beenden auf dem gleichen Weg die Häufigkeiten wieder auf \(\boxed{Aus}\) stellen.
Nun gehen wir in den Statistikbereich unter dem \(\boxed{MENU}\). Wir gehen nach rechts mit den Pfeiltasten

\(\\\)
bis

\(\\\)
erscheint und bestätigen mit \(\boxed{=}\).

\(\\\)
Wir wählen \(\boxed{1}\)

\(\\\)
Wir füllen die Tabelle aus mit den Werten der Beispielaufgabe aus
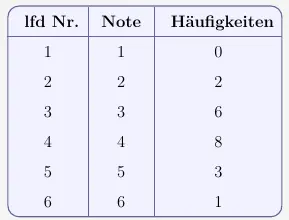
\(\\\)
und haben dann folgende Anzeige:

\(\\\)
Zur Auswertung betätigen wir \(\boxed{OPTN}\)

\(\\\)
und wählen \(\boxed{3}\) und erhalten eine Reihe von Werten:

\(\\\)
Weitere Werte sehen wir mit


\(\\\)
und noch einmal


\(\\\)
Uns interessieren dieses Mal nur folgende Daten, vergleiche dazu die Rechnung per Hand.
\( \begin{array}{ l r c l } \textrm{Anzahl der Schüler :} & \quad n & = & 20 \\[6pt] \textrm{Summe aller Noten :} & \quad \sum x & = & 75 \\[6pt] \textrm{arithmetisches Mittel :} & \quad \overline{x} & = & 3{,}75 \\[6pt] \textrm{Varianz :} & \quad \sigma^2 x & = & 0{,}9875 \\[6pt] \textrm{Standardabweichung :} & \quad \sigma x & = & 0{,}9937303457 \\ \end{array} \)
\(\\[1em]\)
Zusatz für Studenten
Im Studium wird noch unterschieden, ob es sich um eine Vollerhebung oder um eine Stichprobenuntersuchung handelt. Bei Stichproben verwenden wir die Varianz mit
\( \quad \begin{array}{ r c l } V(x) & = & \frac{1}{n-1} \cdot \displaystyle{\sum}_{i=1}^n (x_i - \mu)^2 \cdot h(x_i) \\ \end{array} \)
\(\\\)
statt mit
\( \quad \begin{array}{ r c l } V(x) & = & \frac{1}{n} \cdot \displaystyle{\sum}_{i=1}^n (x_i - \mu)^2 \cdot h(x_i) \\ \end{array} \)
\(\\\)
berechnet. Das hat nun Auswirkungen auf unsere Ergebnisse. In diesem Fall lesen wir die Werte
\(\\\)
\( \begin{array}{ l r c l } \textrm{Anzahl der Schüler :} & \quad n & = & 20 \\[6pt] \textrm{Summe aller Noten :} & \quad \sum x & = & 75 \\[6pt] \textrm{arithmetisches Mittel :} & \quad \overline{x} & = & 3{,}75 \\[6pt] \textrm{Varianz :} & \quad s^2 x & = & 1{,}039473684 \\[6pt] \textrm{Standardabweichung :} & \quad sx & = & 1{,}9019545823 \\ \end{array} \)
\(\\\)
ab.
\(\\[1em]\)