HMF 6 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Zahl a
Um die Zahl \(a\) zu bestimmen, setzen wir den Punkt \(P\) in die Ebene \(E\) ein:
\( \quad \begin{array}{ r c l l } 2a + 2 \cdot 0 -1 & = & 3 \\[6pt] 2a -1 & = & 3 & | + 1 \\[6pt] 2a & = & 4 & | : 2 \\[6pt] a & = & 2 \\ \end{array} \)
\(\\[2em]\)
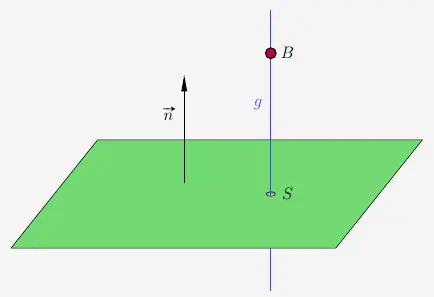
Aufgabe 2 – Schnittpunkt S
Die Gerade \(g\) wird bestimmt mit dem Punkt \(B\) und dem Normalenvektor der Ebene \(E\).
\( \quad \begin{array}{ r c l l } g: \; \vec{x} & = & \vec{b} + t \cdot \vec{n} \\[10pt] & = & \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 3 \\ 4 \end{array} \right) \end{smallmatrix} +t \cdot \begin{smallmatrix} \left( \begin{array}{r} 2 \\ 2 \\ 1 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Aus der Geradengleichung erhalten wir die einzelnen Komponenten
\( \quad \begin{array}{ r c l l } x_1 & = & 1 + 2 t \\[6pt] x_2 & = & 3 + 2 t \\[6pt] x_3 & = & 4 + \; t \\ \end{array} \)
\(\\\)
Zur Schnittpunktberechnung mit der Ebene setzen wir diese in die Ebene \(E\) ein.
\( \quad \begin{array}{ r c l l } 2 \cdot (1 + 2 t) + 2 \cdot (3 + 2 t) + 4 + t & = & 3 \\[6pt] 2 + 4t + 6 + 4t + 4 + t & = & 3 \\[6pt] 9t + 12 & = & 3 & | - 12\\[6pt] 9t & = & -9 & | : 9 \\[6pt] t & = & - 1 \\ \end{array} \)
\(\\\)
\(t\) eingesetzt in die Gerade \(g\) ergibt den Ortsvektor vom Schnittpunkt \(S\).
\( \quad \begin{array}{ r c l c l } \vec{s} & = & \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 3 \\ 4 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{r} 2 \\ 2 \\ 1 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \right) \end{smallmatrix}\\ \end{array} \)
\(\\\)
Der Schnittpunkt lautet also \(S(-1|1|3)\).
\(\\\)