Definition von Funktionen
Inhaltsverzeichnis
\(\\\)
Eine Funktion ist eine Zuordnung und beschreibt die Beziehung zwischen 2 Mengen, der Definitionsmenge und der Wertemenge. Dabei wird einem Element \(x\) aus der Definitionsmenge \(\mathbb{D}\) eindeutig ein Element \(y\) aus der Wertemenge \(\mathbb{W}\) zugeordnet.
Was heißt das nun genau? Zunächst wird einem \(x\) ein \(y\) zugeordnet, wie hier dargestellt:

Die Zuordnung geht von \(x\) nach \(y\). Genau dann, wenn es zu einem \(x\) nur ein \(y\) gibt, wird die Zuordnung als Funktion bezeichnet. Es gibt also auch Zuordnungen, die keine Funktion sind, siehe unten Beispiel 2.
\(\\[2em]\)
Graphische Veranschaulichung
Beispiel 1
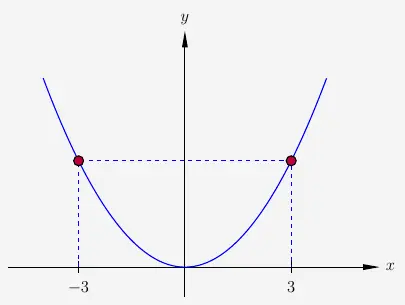
Hier liegt eine Funktion vor, denn zu jedem \(x\) existiert genau ein \(y\). Zu einem \(y\) gibt es zwar zwei \(x\)-Werte, was per Definition aber auch erlaubt ist.
Darüber hinaus können wir sehen, dass in einem Koordinatensystem neue Elemente entstehen, die Punkte eines Graphen. Punkte werden durch Tupel, also Elemente, in denen andere Elemente in geordneter Weise vorliegen, gebildet. Dabei nennt man das Tupel im 2-dimensionalen Koordinatensystem ein Dupel mit \((x|y)\) und das Tupel im 3-dimensionalen Koordinatensystem ein Tripel mit \((x|y|z)\).
\(\\\)
Beispiel 2
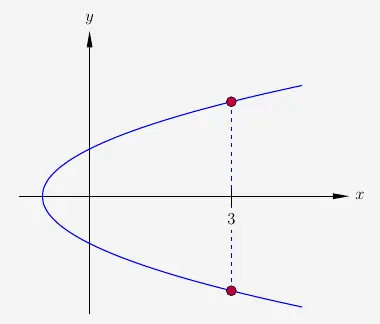
Hier liegt keine Funktion vor. Denn es gibt mindestens ein \(x\), dem mehrere \(y\) zugeordnet sind. Das ist nach der Definition nicht zulässig.
\(\\[2em]\)
Darstellungsformen
Eine Funktion kann auf folgende Arten dargestellt werden:
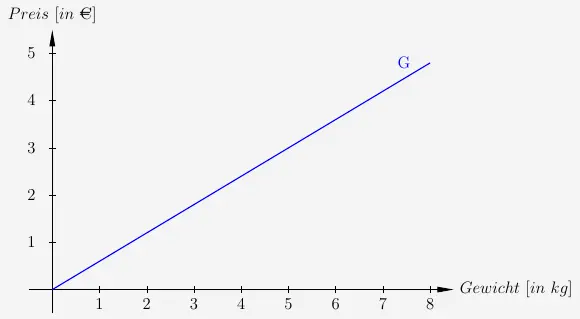
Als Beispiel soll der Preis von Weizen in Abhängigkeit vom Gewicht durch eine lineare Funktion \(f\) repräsentiert werden.
\(\\[2em]\)
Wertetabelle
In der Wertetabelle wird die Zuordnung der \(x\)-Werte und \(y\)-Werte für eine Reihe von Werten erfasst, wobei die Abstände der \(x\)-Werte meist (aber nicht immer) gleichmäßig sind.

\(\\[2em]\)
Funktionsvorschrift
Wesentlich genauer als eine Wertetabelle beschreibt die Funktionsvorschrift, oder auch Funktionsgleichung, die Funktion. Denn diese ist allgemeingültig für alle \(x\)-Werte. Für die Funktion \(f\) wäre eine übliche Schreibweise

Die Bezeichnung der Funktionsgleichung ist in diesem Fall also \(f(x)\).
Die obige Schreibweise ist nun folgendermaßen zu lesen:
f mit f von × ist gleich 0,6 x
\(\\[2em]\)
Graph
Die Bezeichnung des Graphen ist meist genauso wie der der Funktion. Bei einer Funktion \(f\) heißt der Graph dann auch \(f\).
Um deutlich zu machen, dass der Name, der am Graphen steht, nicht der Name der Funktion, sondern des Graphen ist, nenne ich hier den Graphen G.
\(\\[1em]\)