Funktion f
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Punkt A
Wir definieren zunächst die Funktion \(f\).
Beachte: Der Mal-Punkt muss bei der Definition mitgeschrieben werden.

\(\\\)
Die Höhe wird mit

\(\\\)
berechnet. Die Höhe ist also \(5{,}77 \, m\). Die Steigung im Punkt \(A\) berechnen wir mit der 1. Ableitung von \(f\).

\(\\[2em]\)
Aufgabe 2 – Breite des Deiches
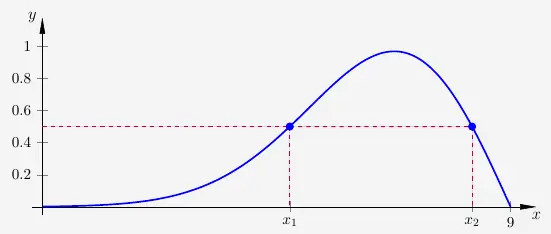
Für die Breite lösen wir die Gleichung
\( \quad f(x) \; = \; 0{,}5 \)
\(\\\)
und verwenden den Solve-Befehl mit

\( \quad 8{,}260201543 - 4{,}755249463 \; \approx \; 3{,}50495208 \)
\(\\\)
Der Deich ist in dieser Höhe ungefähr \(35 \; m\) breit.
\(\\[2em]\)
Aufgabe 3 – Deichhöhe
Die größte Höhe des Deiches liegt im Hochpunkt der Funktion \(f\).
notwendige Bedingung
\( \quad f'(x)=0 \)
\(\\\)
Wir lösen die Gleichung.

\(\\\)
\(11{,}23606798\) liegt außerhalb des Definitionsbereichs mit \(0 \leq x \leq 9\) und kommt als gesuchter \(x\)-Wert nicht infrage.
\(\\[2em]\)
hinreichende Bedingung
\( \quad f''(x) \not= 0 \)
\(\\\)
Wir überprüfen dann \(x=6{,}763932023\) mit der 2. Ableitung vom \(f\).

\(\\\)
\(f''(6{,}763932023) < 0\). Also liegt bei \(x=6{,}763932023\) ein Hochpunkt vor.
\(\\[2em]\)
Funktionswert

\(\\\)
Die Deichhöhe beträgt \(9{,}68 \, m\) .
\(\\\)