Funktion f
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Funktionswert und mittlere Steigung
Funktionswert
\( \quad \begin{array}{ r c c c c c c c l } f(1) & = & 1 \cdot e^{-\frac{1}{2} \cdot 1^2 + \frac{1}{2}} & = & e^{-\frac{1}{2} + \frac{1}{2}} & = & e^0 & = & 1 \\ \end{array} \)
\(\\[1em]\)
Mittlere Steigung
Ist der Graph symmetrischbezüglich des Koordinatenurprungs, so muss der Punkt \((0|0)\) auf dem Graphen liegen. Die mittlere Steigung wird nun ermittelt mit
\( \quad \begin{array}{ r c c c c c c c l } m & = & \frac{f(x_2) - f(x_1)}{x_2 - x_1} & = & \frac{1 - 0}{1 - 0} & = &\frac{1}{1} & = & 1 \\ \end{array} \)
\(\\[2em]\)
Aufgabe 2 – Punktprobe
\( \quad \begin{array}{ r c c c c c l } f(0{,}5) & = & 0{,}5 \cdot e^{-\frac{1}{2} \cdot 0{,}5^2 + \frac{1}{2}} & = & \frac{1}{2} \cdot e^{\frac{3}{8}} & \approx & 0{,}7275 & \not= & 0{,}5 \\ \end{array} \)
\(\\\) Punkt \((0{,}5|0{,}5)\) liegt nicht auf dem Graphen von \(f\).
\(\\[2em]\)
Aufgabe 3 – Nullstelle und Grenzwert
Nullstelle
Es gilt
\( \quad f'(x) \; = \; 0 \)
\(\\\)
Bei
\( \quad f(x) \; = \; x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \)
\(\\\)
ist mit dem Nullprodukt bei
\( \quad x \; = \; 0\)
und/oder
\( \quad e^{-\frac{1}{2}x^2 + \frac{1}{2}} \; = \; 0\) .
\(\\\)
Da nun \(e^{-\frac{1}{2}x^2 + \frac{1}{2}}\) stets größer als Null ist, bleibt nur \(x = 0\) als Lösung.
\(\\[1em]\)
Grenzwert
Wir formen
\( \quad \lim \limits_{x \to \infty} f(x) \; = \; \lim \limits_{x \to \infty} \left(x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \right) \)
\(\\\)
mit dem 1. Potenzgesetz um:
\( \quad \begin{array}{ r c l l } \lim \limits_{x \to \infty} \left( x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \right) & = & \lim \limits_{x \to \infty} \left( x \cdot \dfrac{e^{\frac{1}{2}}}{e^{\frac{1}{2}x^2}} \right) & \rightarrow \; \scriptstyle{\text{Grenzwert aufteilen}} \\[12pt] & = & \lim \limits_{x \to \infty} x \cdot \dfrac{\lim \limits_{x \to \infty} e^{\frac{1}{2}}}{\lim \limits_{x \to \infty} e^{\frac{1}{2}x^2}} & \rightarrow \; \scriptstyle{\text{Grenzwert vom Zähler berechnen}} \\[12pt] & = & \lim \limits_{x \to \infty} x \cdot \dfrac{e^{\frac{1}{2}}}{\lim \limits_{x \to \infty} e^{\frac{1}{2}x^2}} & \rightarrow \; \scriptstyle{\text{Vorfaktor und Zähler tauschen}} \\[12pt] & = & e^{\frac{1}{2}} \cdot \dfrac{\lim \limits_{x \to \infty} x}{\lim \limits_{x \to \infty} e^{\frac{1}{2}x^2}} & \rightarrow \; \scriptstyle{\text{Potenz umformen}} \\[12pt] & = & \sqrt{e} \cdot \dfrac{\lim \limits_{x \to \infty} x}{\lim \limits_{x \to \infty} e^{\frac{1}{2}x^2}} \\[12pt] \end{array} \)
\(\\\)
Der Faktor \(\sqrt{e}\) ist hier vernachlässigbar. Der Term
\( \quad \dfrac{\lim \limits_{x \to \infty} x}{\lim \limits_{x \to \infty} e^{\frac{1}{2}x^2}} \)
\(\\\)
ist von der Form \(\frac{\infty}{\infty}\). Das ist so nicht lösbar, jedoch schon mit dem Satz von l’Hopital. Vereinfacht kann man aber auch sagen, dass die e-Funktion dominierend ist. Es ist also nur
\( \quad \dfrac{1}{\lim \limits_{x \to \infty} e^{\frac{1}{2}x^2}} \)
\(\\\)
zu lösen. Da nun
\( \quad \dfrac{1}{\lim \limits_{x \to \infty} e^x} \; = \; \lim \limits_{x \to \infty} \frac{1}{e^x} \; = \; 0 \)
\(\\\)
ist, ist auch
\( \quad \dfrac{1}{\lim \limits_{x \to \infty} e^{\frac{1}{2}x^2}} \; = \; \lim \limits_{x \to \infty} \dfrac{1}{e^{\frac{1}{2}x^2}} \; = \; 0 \)
\(\\\)
Das heißt nun für das Randverhalten, dass wenn wir uns auf dem Graphen immer weiter nach rechts bewegen, \(f(x)\) gegen Null strebt, also der \(x\)-Achse entgegen.
\(\\[2em]\)
Aufgabe 4 – Ableitungsterm
\( \quad f(x) \; = \; x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \)
\(\\\)
ist eine Produktfunktion von der Form
\( \quad f(x) \; = \; u(x) \cdot v(x) \)
\(\\\)
Wir leiten diese mit der, hier in der vereinfachten Schreibweise, Produktregel
\( \quad f(x) \; = \; u' \cdot v + u \cdot v' \)
\(\\\)
ab. Dabei ist
\( \quad \begin{array}{ r c l l } u & = & x \\[6pt] v & = & e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\ \end{array} \)
\(\\\)
\(v\) ist eine verkettete Funktion und wird generell mit der Kettenregel abgeleitet,vergleiche meine früheren Abiturlösungen. Bei \(e\)-Funktion kann eine vereinfachte Kettenregel angewandt werden mit
\( \quad \begin{array}{ r c l l } v & = & e^{g(x)} \\[6pt] v' & = & g'(x) \cdot e^{g(x)} \\ \end{array} \)
\(\\\)
Daraus ergibt sich
\( \quad \begin{array}{ r c l l } u & = & x \\[6pt] u' & = & 1 \\[12pt] v & = & e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\[6pt] v' & = & -x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\ \end{array} \)
\(\\\)
Es folgt
\( \quad \begin{array}{ r c l l } f'(x) & = & 1 \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} + x \cdot \left( - x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \right) \\[8pt] & = & 1 \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} - x^2 \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\[8pt] & = & \left(1 - x^2\right) \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\ \end{array} \)
\(\\[2em]\)
Aufgabe 5 – Monotonieverhalten
Das Monotonieverhalten ändert sich in den Extremstellen. Deshalb sind diese zunächst zu bestimmen.
\(\\\)
Notwendige Bedingung
\( \quad \begin{array}{ r c l } f'(x) & = & 0 \\[16pt] 0 & = & \left(1 - x^2\right) \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\[8pt] & \Leftrightarrow & 0 = 1 - x^2\quad \wedge \quad 0 = e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\ \end{array} \)
\(\\\)
Es sind nun beide Fälle zu untersuchen.
\( \quad \begin{array}{ r c l l } e^{-\frac{1}{2}x^2 + \frac{1}{2}} & \not= & 0 & \text{(keine Lösung)}\\[8pt] 0 & = & 1 - x^2 & \bigl| + x^2 \\[8pt] x^2 & = & 1 & \bigl| \sqrt{\dots} \\[8pt] x_1 & = & -1 \\[6pt] x_2 & = & 1 \\ \end{array} \)
\(\\\)
Hinreichende Bedingung
\( \quad \begin{array}{ r c l } f''(x) & \not= & 0 \\[16pt] f''(x) & = & u' \cdot v + u \cdot v' \\[16pt] & & \qquad u \; = \; 1 - x^2 \\[8pt] & & \qquad u' \; = \; -2x \\[8pt] & & \qquad v \; = \; e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\[8pt] & & \qquad v' \; = \; - x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \\[16pt] f''(x) & = & -2x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} +\left(1 - x^2\right) \cdot \left( - x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \right) \\[16pt] f''(1) & = & -2 \cdot 1 \cdot e^{-\frac{1}{2} \cdot 1^2 + \frac{1}{2}}+\left(1 - \cdot 1^2\right) \cdot \left( - 1 \cdot e^{-\frac{1}{2} \cdot 1^2 + \frac{1}{2}} \right) \\[8pt] & = & -2 \cdot e^0 + 0 \cdot \left( - 1 \cdot e^0 \right) \\[8pt] & = & -2 \cdot 1 + 0 \cdot ( - 1) \\[8pt] & = & -2 \; < \; 0 \\[8pt] & \Rightarrow & \text{Hochpunkt bei }\; x=1 \\[16pt] f''(-1) & = & -2 \cdot (-1) \cdot e^{-\frac{1}{2} \cdot (-1)^2 + \frac{1}{2}} +\left(1 - (-1)^2\right) \cdot \left( - (-1) \cdot e^{-\frac{1}{2} \cdot (-1)^2 + \frac{1}{2}} \right) \\[8pt] & = & 2 \cdot e^0 + 0 \cdot \left( 1 \cdot e^0 \right) \\[8pt] & = & 2 \cdot 1 + 0 \cdot 1 \\[8pt] & = & 2 \; > \; 0 \\[8pt] & \Rightarrow & \text{Tiefpunkt bei }\; x=-1 \\ \end{array} \)
\(\\\)
Links vom Tiefpunkt muss der Graph fallend und rechts davon steigend sein. Entsprechend gilt für Hochpunkte, dass ein Graph links davon steigend und rechts davon fallend ist. Das heißt:
\( \quad \begin{array}{ r c l } (\ -\infty ; -1] & : & \scriptstyle{\text{streng monoton fallend (halboffenes Intervall)}} \\[6pt] (\ -1 ; 1] & : & \scriptstyle{\text{streng monoton steigend (halboffenes Intervall)}} \\[6pt] (\ 1 ; \infty) & : & \scriptstyle{\text{streng monoton fallend (offenes Intervall)}} \\[6pt] \end{array} \)
\(\\[2em]\)
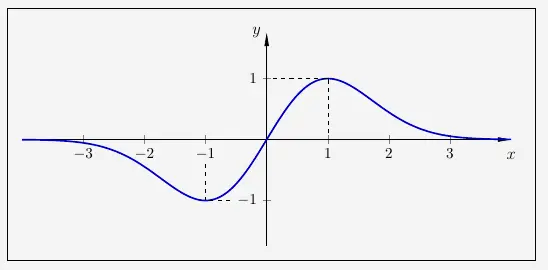
Aufgabe 6 – Koordinatenachsen
Für die Skalierung der Koordinatenachsen benötigen wir noch die Höhen der Extrempunkte. In der 1. Teilaufgabe (Funktionswert) wurde bereits festgestellt, dass \(f(1)=1\) ist. Wegen der Punktsymmetrie muss deshalb auch \(f(-1)=-1\) sein.
Wir haben damit den Tiefpunkt \(T(-1|-1)\) und den Hochpunkt \(H(1|1)\).
\(\\\)