Datenschutzbedenken
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Baumdiagramm
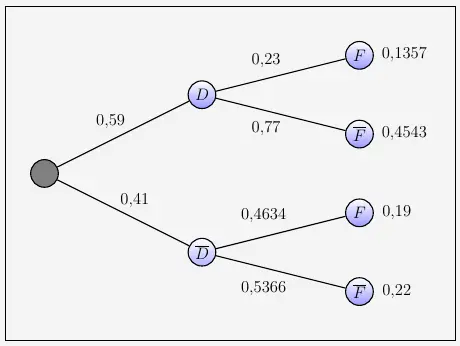
\(\\[2em]\)
Aufgabe 2 – Kein Fitnessarmband und Datenschutzbedenken
Dies ist die Wahrscheinlichkeit eines zweistufigen Zufallsexperiment und wird mit der Multiplikationsregel berechnet.
\( \quad \begin{array}{ r c l } P( \overline{F} \cap D ) & = & P( \overline{F} ) \cdot P( D ) \\[6pt] & = & P( D ) \cdot P_D( \overline{F} ) \\[6pt] & = & P( D ) \cdot \big( 1 - P_D( F ) \big) \\[6pt] & = & 0{,}59 \cdot (1 - 0{,}23) \\[6pt] & = & 0{,}59 \cdot 0{,}77 \\[6pt] & = & 0{,}4543 \\[6pt] & = & 45{,}43 \, \% \\ \end{array} \)
\(\\[2em]\)
Aufgabe 3 – Bedingte Wahrscheinlichkeit
In diesem Fall liegt die Voraussetzung ,,Fitnessarmband’‘ \((F)\) vor und wir berechnen die Wahrscheinlichkeit mit
\( \quad \begin{array}{ r c l } P_F( D ) & = & \dfrac{P( F \cap D )}{P( F )} \\[10pt] & = & \dfrac{P( D \cap F )}{P( D \cap F ) + P( \overline{D} \cap F )} \\[10pt] & = & \dfrac{P(D) \cdot P_D(F)}{P(D) \cdot P_D(F) + P( \overline{D} \cap F )} \\[10pt] & = & \dfrac{0{,}59 \cdot 0{,}23}{0{,}59 \cdot 0{,}23 + 0{,}19} \\[8pt] & = & 0{,}4166 \\[8pt] & = & 41{,}66 \, \% \\ \end{array} \)
\(\\[2em]\)
Aufgabe 4 – Stochastische Abhängigkeit
Es gilt, wie in der vorherigen Aufgabe gezeigt wurde,
\( \quad P(F) \; = \; 0{,}59 \cdot 0{,}23 + 0{,}19 \)
\(\\\)
und darüber hinaus
\( \quad P_D(F) \; = \; 0{,}23 \)
\(\\\)
Ist die Wahrscheinlichkeit für
,,Der Versicherte benutzt ein Fitnessarmband’‘
unabhängig davon, ob der Versicherte Datenschutzbedenken hat oder nicht, so muss gelten
\( \quad P_D(F) \; = \; P(F) \)
\(\\\)
Dies ist hier nicht der Fall, denn es gilt ja
\( \quad \begin{array}{ r c l } 0{,}23 & \not= & 0{,}59 \cdot 0{,}23 + 0{,}19 \end{array} \)
\(\\\)
Folglich sind die Ereignisse \(F\) und \(D\) stochastisch abhängig.
\(\\[2em]\)
Aufgabe 5 – Binomialverteilung
Das Ereignis \(D\) ist binomialverteilt, denn
- es gibt nur die Merkmalsausprägungen
- ,,Der Versicherte hat Datenschutzbedenken.‘’
- ,,Der Versicherte hat keine Datenschutzbedenken.‘’
- das Ereignis kann wie ein Fall mit Zurücklegen berechnet werden. Es ist zwar ein Fall ohne Zurücklegen, denn ein Versicherten wird ja nicht mehrmals ausgewählt. Ist aber da die Stichprobe (100 Versicherte) im Verhältnis zu der Grundmenge (alle Versicherte der Krankenversicherung) relativ klein ist, so darf die Berechnung mit der Binomialverteilung durchgeführt werden.
Darüber hinaus ist die Grundmenge hier auch nicht angegeben und es stehen nur Wahrscheinlichkeiten in Prozenten zur Verfügung. Es ist also nur die Berechnung mit der Binomialverteilung möglich.
\(\\[1em]\)
Höchstens 70
Wir berechnen die kumulierte (aufsummierte) Binomialverteilung mit
\( \quad P(x\leq k) = \displaystyle{\sum\limits_{i=1}^k} \begin{smallmatrix} \left( \begin{array}{c} n \\ i \end{array} \right) \end{smallmatrix} p^i \cdot (1-p)^{n-i}. \)
\(\\\)
Wir benötigen also \(n\), \(p\) und \(k\) und wählen
\( \quad \begin{array}{ r c l } n & = & 100 \\[6pt] p & = & 0{,}59 \\[6pt] k & \leq & 70 \\ \end{array} \)
\(\\\)
Hier von \(x=40\) bis \(x=78\) dargestellt:
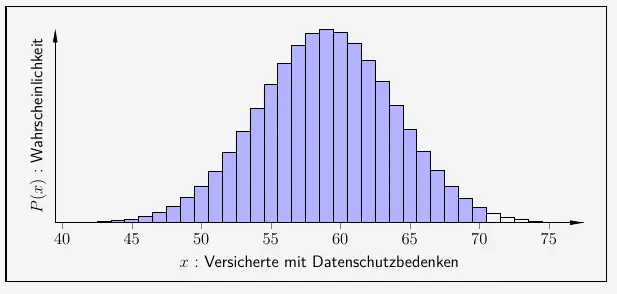
\( \quad \begin{array}{ r c l c l } P(x \leq 70) & = & 0{,}9913 & = & 99{,}13 \% \\ \end{array} \)
\(\\[1em]\)
Mehr als 50
Hier gilt \(k > 50\).
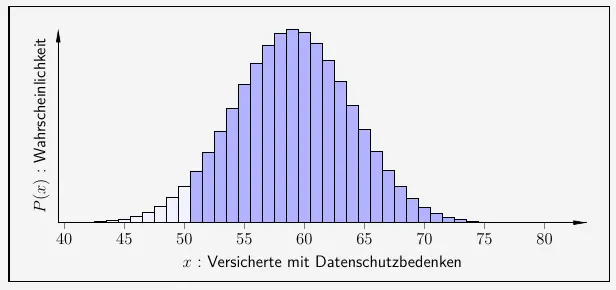
\( \quad \begin{array}{ r c l } P(x > 50) & = & 1 - P(x \leq 50) \\[6pt] & = & 1 - 0{,}0428 \\[6pt] & = & 0{,}9572 \\[6pt] & = & 95{,}72 \% \\ \end{array} \)
\(\\[1em]\)
Mindestens 54 und höchstens 64
Hier gilt jetzt \(54 \leq k \leq 64\).
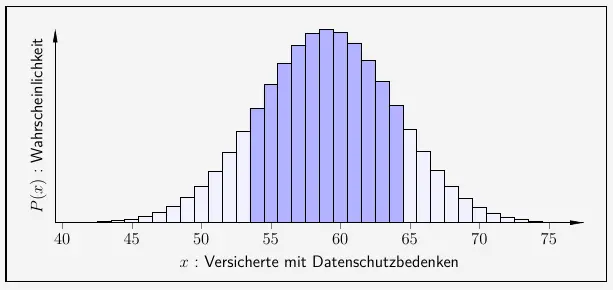
\( \quad \begin{array}{ r c l } P(54 \leq k \leq 64) & = & P(x \leq 64) - P(x \leq 53) \\[6pt] & = & 0{,}8687 - 0{,}132 \\[6pt] & = & 0{,}7367 \\[6pt] & = & 73{,}67 \% \\ \end{array} \)
\(\\[2em]\)
Aufgabe 6 – Platzhalter a und b
Verwenden wir in dem Term
\( \quad \displaystyle{\sum\limits_{k=51}^{100}} \binom{100}{k} \cdot 0{,}59^k \cdot a^b \)
\(\\\)
die Platzhalter
\( \quad a \; =\; 1 - 0{,}59 \; =\; 0{,}41 \)
\(\\\)
und
\( \quad b \; =\; 100-k \, , \)
\(\\\)
so wäre
\( \quad \displaystyle{\sum\limits_{k=51}^{100}} \binom{100}{k} \cdot 0{,}59^k \cdot a^b \; =\; \displaystyle{\sum\limits_{k=51}^{100}} \binom{100}{k} \cdot 0{,}59^k \cdot 0{,}41^{100-k} \; =\; P(x \geq 51) \)
\(\\\)
eine kumulierte Binomialverteilung mit \(n=100\) und \(p=0{,}59\). Diese drückt aus, dass sich unter \(100\) ausgewählten Versicherten mindestens \(51\) mit Datenschutzbedenken befinden. Der Term
\( \quad \begin{array}{ r c l } 1- \displaystyle{\sum\limits_{k=51}^{100}} \binom{100}{k} \cdot 0{,}59^k \cdot a^b & = & 1- \displaystyle{\sum\limits_{k=51}^{100}} \binom{100}{k} \cdot 0{,}59^k \cdot 0{,}41^{100-k} \\[10pt] & = & 1 - P(x \geq 51) \\[6pt] & = & P(x \leq 50) \\ \end{array} \)
\(\\\)
dagegen beschreibt das Ereignis, dass sich unter \(100\) zufällig ausgewählten Versicherten höchstens \(50\) mit Datenschutzbedenken befinden.
\(\\\)