Aufgaben
Inhaltsverzeichnis
\(\\\)
“E-Funktionen (CAS)”
Gegeben ist die Schar der in \(\mathbb{R}\) definierten Funktionen \(f_a\) mit
\( \quad f_a(x) \; = \; x \cdot e^{-\frac{1}{2} a \cdot x^2 + \frac{1}{2}} \quad \textit{und} \quad a \in \mathbb{R} \)
Die zugehörigen Graphen sind symmetrisch bezüglich des Koordinatenursprungs.
\(\\[1em]\)
Funktionen der Schar
Zunächst werden einzelne Funktionen der Schar betrachtet.
\(\\\)
- Berechnen Sie die Koordinaten des Hochpunktes des Graphen von \(f_1\).
(4 P)
\(\\\)
- Weisen Sie nach, dass \(f_1\) genau eine Nullstelle hat, und geben Sie den Grenzwert von \(f_1\) für \(x \rightarrow +\infty\) an.
(2 P)
\(\\\)
-
Die Abbildung 1 zeigt den Graphen von \(f_1\) ohne das zugrunde liegende Koordinatensystem.
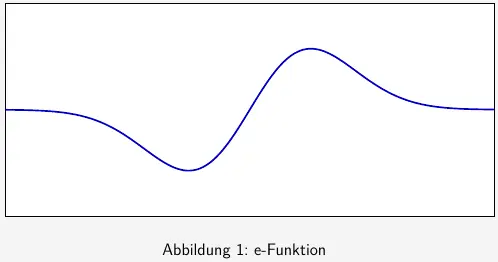
\(\qquad \qquad \qquad\)Ergänzen Sie die Koordinatenachsen und skalieren Sie diese passend.
(2 P)
\(\\\)
-
Interpretieren Sie den folgenden Sachzusammenhang geometrisch:
Für jede Stammfunktion \(F_1\) von \(f_1\) und für jede reelle Zahl \(u>2022\) gilt
\(\quad F_1(u) - F_1(0) \; \approx \; \displaystyle{\int}_0^{2022} f_1(x) dx \)
(3 P)
\(\\\)
- Der Graph von \(f_0\) ist eine Gerade. Geben Sie die Steigung dieser Gerade und die Koordinaten ihres Schnittpunkts mit der \(y\)-Achse an.
(2 P)
\(\\\)
- Für einen Wert von \(a\) liegt der Punkt \(P(1|e)\) auf dem Graphen von \(f_a\).
Berechnen Sie für diesen Wert von \(a\) die Größe des Winkels, den der Graph von \(f_a\) mit der Parallele zur \(x\)-Achse durch den Punkt \(P\) einschließt.(4 P)
\(\\\)
-
Begründen Sie unter Verwendung der Abbildung 2, dass
\( \quad \displaystyle{\int}_{-0{,}5}^1 f_{-1}(x) dx \; = \; \displaystyle{\int}_{0{,}5}^1 f_{-1}(x) dx \)
gilt.
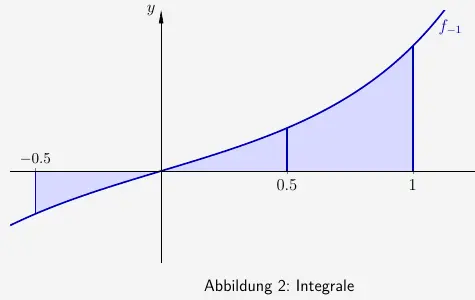
(2 P)
\(\\[2em]\)
Aussagen
Nun werden alle Funktionen der gegebenen Schar betrachtet.
\(\\[1em]\)
-
Die folgenden Aussagen gelten für alle Zahlen \(a\), \(a_1\) und \(a_2\):
-
\(f_a(0) = 0\)
-
\(f_a'(0) = f_0'(0)\)
-
\(f_{a_1}(x) = f_{a_2}(x) \quad \Leftrightarrow \quad a_1 = a_2 \; \vee \; x = 0\)
Geben Sie an, was sich aus diesen Aussagen hinsichtlich des Verlaufs der Graphen der Schar folgern lässt.
(3 P)
-
\(\\\)
- Zeigen Sie, dass die folgende Aussage für jeden Wert von \(a\) richtig ist:
,,Wird der Graph von \(f_a\) mit dem gleichen Faktor \(k>0\) sowohl in \(x\)-Richtung als auch in \(y\)-Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.‘’
(3 P)
\(\\\)
-
Für jedes \(a \in \mathbb{R}\setminus{\{0\}}\) sind die Wendestellen von \(f_a\) genau die Lösungen der Gleichung
\(\quad ( a \cdot x^2 - 3) \cdot x \; = \; 0 . \)
Geben Sie für alle Werte von \(a \in \mathbb{R}\) die Anzahl der Wendestellen von \(f_a\) an und begründen Sie Ihre Angabe.
(5 P)
\(\\[2em]\)
Extrempunkte der Schar
-
Zeigen Sie, dass alle Extrempunkte der Graphen der Schar auf der Gerade mit der Gleichung
\( \quad y \; = \; x \)
liegen.
(5 P)
\(\\\)
-
Für jeden positiven Wert von \(a\) bilden der Hochpunkt \(\big( v|f_a(v) \big)\) des Graphen \(f_a\), der Punkt \((0|2)\), der Koordinatenursprung und der Punkt \((v|0)\) die Eckpunkte eines Vierecks.
Bestimmen Sie ausgehend von einer geeigneten Skizze denjenigen Wert von \(a\), für den das Viereck den Flächeninhalt \(144\) hat.
(5 P)
\(\\[2em]\)