Scheitelpunktform
Inhaltsverzeichnis
\(\\\)
Allgemeine Form in Scheitelpunktform
Als dem Scheitelpunkt bezeichnet man den Punkt, wo der Verlauf der Parabel von fallend nach steigend bzw. von steigend nach fallend wechselt. Also ist der Scheitelpunkt bei nach oben geöffneten Parabeln der tiefste Punkt und bei nach unten geöffneten Parabeln der höchste Punkt.
Bei der Normalparabel liegt der Scheitelpunkt im Koordinatenursprung.
Ist der Scheitelpunkt nun aus dem Koordinatenursprung verschoben, so kann man den Scheitelpunkt \(S(d | e)\) in der Scheitelpunktform
\( \quad f(x) \, = \, a \left(x - d\right)^2 + e \)
\(\\\)
direkt ablesen.
In der Regel liegt die quadratische Funktionsgleichung in der allgemeinen Form
\( \quad f(x) \, = \, ax^2 + bx + c \)
\(\\\)
vor.
Wie kommt man nun von der allgemeinen Form in die Scheitelpunktform?
Dazu benötigen wir die ersten beiden binomischen Formeln:
\(\\\)
\(\quad \begin{array}{ r c l l } 1. & (a + b)^2 & = & a^2 \; + \; 2ab \; + \; b^2 \\[5pt] 2. & (a - b)^2 & = & a^2 \; - \; 2ab \; + \; b^2 \\ \end{array}\)
\(\\\)
Beispiel:
\( \quad f(x) \, = \, x^2 - 4x + 9 \)
\(\\\)
Zunächst muss bei der Scheitelpunkt der Teil
\( \quad (x - d)^2 \)
\(\\\)
bestimmt werden. Genauer gesagt, dass \(x\) und das \(d\) werden gesucht.
Offensichtlich entspricht der Term
\( \quad x^2 - 4x + 9 \)
\(\\\)
dem Term der zweiten binomischen Formel
\( \quad a^2 - 2ab + b^2 \)
\(\\\)
Darüber kann nun auf \(a\) und \(b\) und damit auf den linken Teil
\( \quad (a - b)^2 \)
\(\\\)
der binomischen Formel geschlossen werden.
Es ist leicht zu erkennen, dass
\( \quad a^2 = x^2 \quad \Leftrightarrow \quad a = x \)
\(\\\)
ist.
Weiter gilt:
Das \(b\) wird über den Mittelteil \(2ab\) der rechten Seite der binomischen Formel gebildet.
\(\\\)
Da \(a=x\) ist, muss in dem obigen Beispiel gelten
\( \quad 2b = 4 \quad \Leftrightarrow \quad b = 2 \)
\(\\\)
Merke:
Das \(b\) ist stets die Hälfte des Wertes, der vor dem \(x\) steht.
\(\\\)
Die Bestimmung der Scheitelpunktform erfolgt nun auf folgende Weise:
\(\\[2em]\)
Scheitelpunktform bei einer verschobenen Normalparabel
Der Term
\( \quad x^2 - 4x \)
\(\\\)
wird mit der quadratischen Ergänzung zum vollständigen Binom ergänzt.
\( \quad x^2 \; - \; 4x \; \color{green}{+ \; 2^2} \)
\(\\\)
Da die Funktionsgleichung ins Ungleichgewicht kommen würde, wird die Ergänzung gleichzeitig wieder abgezogen.
\( \quad f(x) \; = \; x^2 \; - \; 4x \; \color{green}{\underbrace{+ \; 2^2 \; - \; 2^2}_{0}} \; + \; 9 \)
\(\\\)
Die zum Binom gehörigen Teile können nun umgeformt werden.
\( \quad f(x) \; = \; \color{green}{\underbrace{x^2 \; - \; 4x \; + \; 2^2}_{(x-2)^2}} \; - \; 2^2 \; + \; 9 \)
\(\\\)
Zusammengefasst ergibt sich die Scheitelpunktform
\( \quad f(x) \; = \; (x-2)^2 \; + \; 5 \)
\(\\\)
mit dem Scheitelpunkt \(S(2 | 5)\).
\(\\[1em]\)
Übungen
Zur Einüben und zum Festigen des Verfahrens der quadratischen Ergänzung folgen hier nun einige Aufgaben mit Lösungen.
Stelle die Scheitelpunktform der Funktionsgleichungen
-
\(\; f(x) = x^2 - 6x + 3\)
-
\(\; f(x) = x^2 + 12x + 32\)
-
\(\; f(x) = x^2 - 3x - 0{,}75\)
\(\\\)
auf. Gib auch jeweils die Koordinaten des Scheitelpunktes an.
\(\\[2em]\)
Scheitelpunktform bei einer gestreckten Parabel
Bei einer gestreckten Parabel kommt der Streckungsfaktor mit \(a>1\) vor. Ich wähle hier nun ganzzahlige Werte für \(a\). Zu Brüchen kommen wir später.
Beispiel:
\( \quad f(x) \; = \; 3x^2 - 12x + 7 \)
\(\\\)
Um die quadratische Ergänzung durchführen zu können, muss vorerst die 3 vor dem \(x^2\) ausgeklammert werden. Notwendig ist das Ausklammern nur bei den Teilen, die ein \(x\) enthalten.
\( \quad f(x) \; = \; \color{green}{3 \cdot \left(x^2 - 4x\right)} + 7 \)
\(\\\)
Nun kann die quadratische Ergänzung durchführt werden.
\( \quad f(x) \; = \; 3 \cdot \left( x^2 - 4x \color{green}{ \, + \, 2^2 - 2^2} \right) + 7 \)
\(\\\)
Die zum Binom gehörigen Teile können umgeformt werden.
\( \quad f(x) \; = \; 3 \cdot \Big( \; \color{green}{\underbrace{\left( x^2 - 4x + 2^2\right)}_{(x-2)^2}} - 4 \Big) + 7 \)
\(\\\)
also
\( \quad f(x) \; = \; 3 \cdot \Big( \left( x - 2\right)^2 - 4 \Big) + 7 \)
\(\\\)
Zum Schluss wird ausmultipliziert, so dass der Teil, der nicht zum Binom gehört, also die -4, ohne Klammer steht.
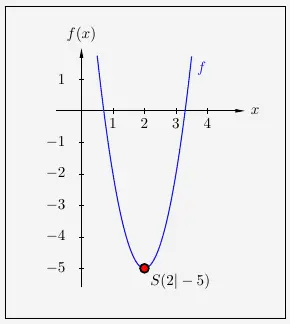
\( \quad \begin{array}{ l } f(x) = 3 \cdot \left( x - 2\right)^2 - 3 \cdot 4 + 7 \\[5pt] f(x) = 3 \cdot \left( x - 2\right)^2 - 5 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Verlauf:
\(\\[1em]\)
Übungen
Stelle die Scheitelpunktform der Funktionsgleichungen
-
\(\; f(x) =2x^2 + 16x + 30\)
-
\(\; f(x) = -2x^2 + 20x -40\)
\(\\\)
Gib auch die Koordinaten der Scheitelpunkte an.
\(\\[2em]\)
Scheitelpunktform mit Brüchen
Bei gestauchten und gestreckten Parabeln kann der Streckungsfaktor \(a\) als Bruch angegeben sein. Bei gestauchten Parabeln ist der Streckungsfaktor in der Regel ein Bruch (oder Dezimalbruch), denn der Streckungsfaktor muss dann ja zwischen -1 und 1 liegen.
Beispiel:
\( \quad f(x) \; = \; \frac{2}{3}x^2 - 4x + 1 \)
Um den Wert für die -4 herauszubekommen, wenn nun die \(\frac{2}{3}\) ausgeklammert wird, multiplizieren wir den Kehrwert von \(\frac{2}{3}\) mit -4.
\( \quad f(x) \; = \; \color{green}{\frac{2}{3} \cdot \left(x^2 - \frac{3}{2} \cdot 4x\right)} + 1 \)
\(\\\)
Es ergibt sich
\( \quad f(x) \; = \; \frac{2}{3} \cdot \left(x^2 - 6x\right) + 1 \)
\(\\\)
Es folgt die quadratische Ergänzung
\( \quad f(x) \; = \; \frac{2}{3} \cdot \left(x^2 - 6x \color{green}{ \, + \, 3^2 - 3^2}\right) + 1 \)
\(\\\)
und die Binomumformung:
\( \quad f(x) \; = \; \frac{2}{3} \cdot \Big( \color{green}{(x - 3)^2} - 9 \Big) + 1 \)
\(\\\)
Schließlich wird wieder ausmultipliziert
\( \quad f(x) \; = \; \color{green}{\frac{2}{3} \cdot (x - 3)^2 - \frac{2}{3} \cdot 9} + 1 \)
\(\\\)
und zusammengefasst.
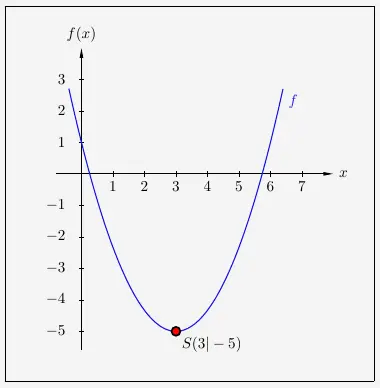
\( \quad f(x) \; = \; \frac{2}{3} \cdot (x - 3)^2 - 5 \)
\(\\\)
Wir erhalten folgenden Graphen:
\(\\[1em]\)
Übungen
Stelle die Scheitelpunktform der Funktionsgleichungen
-
\(\; f(x) =\frac{1}{4}x^2 - x - 2\)
-
\(\; f(x) = \frac{1}{6}x^2 + \frac{1}{3}x -\frac{7}{3}\)
-
\(\; f(x) = -\frac{3}{2}x^2 + \frac{9}{5}x +\frac{223}{50}\)
\(\\\)
Gib auch die Koordinaten der Scheitelpunkte an.
\(\\[2em]\)
Nullstellen bei der Scheitelpunktform
Liegt eine quadratische Gleichung in der Scheitelpunktform vor, so lassen sich die Nullstellen relativ unkompliziert ohne Ausklammern oder PQ-Formel berechnen.
Beispiel:
\( \quad f(x) \; = \; \frac{1}{2} (x + 3)^2 + \frac{5}{2} \)
\(\\\)
Für die Bestimmung der Nullstellen gilt folgende Bedingung:
\( \quad f(x) \; = \; 0 \)
\(\\\)
Einsetzen von \(f(x)\) :
\( \quad \begin{array}{ r c l l } \frac{1}{2} (x - 3)^2 - 2 & = & 0 & | + 2 \\[5pt] \frac{1}{2} (x - 3)^2 & = & 2 & | \cdot 2 \\[5pt] (x - 3)^2 & = & 4 & | \sqrt{\cdots} \\ \end{array} \)
\(\\\)
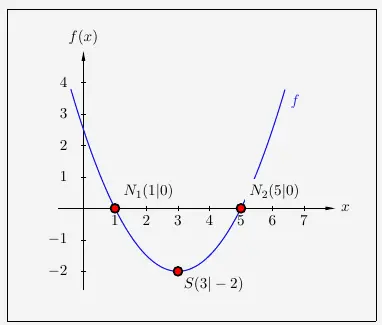
Beim Wurzelziehen entstehen 2 Lösungen :
\( \quad \begin{array}{ r c l l c r c l l } x - 3 & = & -2 & | - 3 & \quad \textrm{und} & \quad x - 3 & = & 2 & | + 3 \\[5pt] x_1 & = & 1 & & & x_2 & = & 5 & \\ \end{array} \)
\(\\[1em]\)
Übungen
Wie lauten die Nullstellen der Funktion
-
\(\; f(x) =(x + 1)^2 - 4\)
-
\(\; f(x) = -\frac{2}{3}(x - 2)^2 + 6\)
\(\\[2em]\)
Umformung Scheitelpunktform in allgemeine Form
Liegt die quadratische Gleichung in der Scheitelpunktform vor, so wird zunächst das Binom mit der 1. bzw. 2. binomischen Formel
\( \quad (a \; \pm \; b)^2 = a^2 \; \pm \; 2ab \; + \; b^2 \)
\(\\\)
aufgelöst.
Beispiel:
\( \quad f(x) \; = \; 3 (x + 5)^2 - 70 \)
\(\\\)
Es gilt
\( \quad \begin{array}{ l } f(x) = 3 (x + 5)^2 - 70 \\[5pt] f(x) = 3 (x^2 + 10 x + 25) - 70 \\[5pt] f(x) = 3 x^2 + 30 x + 75 - 70 \\[5pt] f(x) = 3 x^2 + 30 x + 5 \\ \end{array} \)
\(\\[1em]\)