HMF 2 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Nullstelle der Tangente
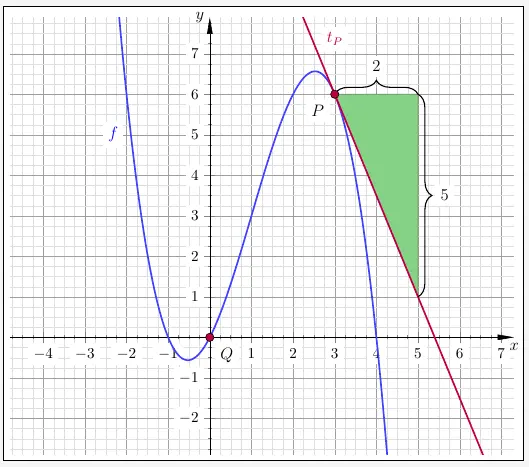
Mit der Steigung \(-\frac{5}{2}\) sieht die Tangente wie folgt aus.
\(\\\)
Die Nullstelle von \(t_P\) liegt bei \(x = 5{,}4\).
\(\\[2em]\)
Aufgabe 2 – Tangente durch P ?
Die Tangente \(t_Q\), die durch den Punkt \(Q(0|0)\) verläuft, ist eine Ursprungsgerade und von der Form
\( \quad t_Q(x) = mx \)
\(\\\)
Die Steigung \(m\) der Tangente wird mit der 1. Ableitung von \(f\) berechnet. Es gilt
\( \quad f'(x) = -\frac{3}{2}x^2 + 3x + 2 \)
\(\\\)
An der Stelle Null erhalten wir
\( \quad m = f'(0) = -\frac{3}{2} \cdot 0^2 + 3 \cdot 0 + 2 = 2 \)
\(\\\)
Es ergibt sich
\( \quad t_Q(x) = 2x \)
\(\\\)
Die Punktprobe mit \(P(3|6)\) ergibt
\( \quad \begin{array}{ r c l } 6 & = & 2 \cdot 3 \\[6pt] 6 & = & 6 \\ \end{array} \)
\(\\\)
Die Gleichung ist wahr. Folglich liegt \(P\) auf der Tangente \(t_Q\).
\(\\\)