Funktion f
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Herleitung der Gleichung
Wir erstellen ein Gleichungssystem und brauchen dazu die allgemeine Gleichung dritten Grades und ihre Ableitung:
\( \quad \begin{array}{ r c l } f(x) & = & ax^3 + bx^2 + cx + d \\[6pt] f'(x) & = & 3ax^2 + 2bx + c \\[6pt] \end{array} \)
\(\\\)
Wir nehmen die angegebenen Punkte und setzen sie in die entsprechende allgemeine Gleichung ein:
\( \quad \begin{array}{ l c r c l } A(0|0{,}2) & \quad \Longrightarrow & f(0) & = & 0{,}2 \\[6pt] B(1|0{,}3) & \quad \Longrightarrow & f(1) & = & 0{,}3 \\[6pt] T(0{,}5|0{,}13) & \quad \Longrightarrow & f(0{,}5) & = & 0{,}13 \\[6pt] & \quad \Longrightarrow & f'(0{,}5)& = & 0 \\ \end{array} \)
\(\\\)
Daraus ergibt sich folgendes Gleichungssystem:
\( \quad \begin{array}{ c*{10}{c} } \textrm{I} & 0{,}2 & = & & & & & & & d \\[6pt] \textrm{II} & 0{,}3 & = & a &+ & b & + & c & + & d \\[6pt] \textrm{III} & 0{,}13 & = & {0{,}5}^3 a & + & {0{,}5}^2 b & + & 0{,}5 c & + & d \\[6pt] \textrm{IV} & 0 & = & 3 \cdot {0{,}5}^2 a & + & 2 \cdot 0{,}5 b & + & c & & \\[25pt] \textrm{I} & 0{,}2 & = & & & & & & & d \\[6pt] \textrm{II} & 0{,}3 & = & a & + & b & + & c & + & d \\[6pt] \textrm{III} & 0{,}13 & = & 0{,}125 a & + & 0{,}25 b & + & 0{,}5 c & + & d \\[6pt] \textrm{IV} & 0 & = & 0{,}75 a & + & b & + & c & & \\ \end{array} \)
\(\\\)
Wir lösen das Gleichungssystem mit dem Taschenrechner und erhalten die Lösungen
\( \quad \begin{align} a & = 0{,}4 \\[6pt] b & = -0{,}12 \\[6pt] c & = -0{,}18 \\[6pt] d & = 0{,}2 \end{align} \)
\(\\\)
Daraus folgt die Funktion \(f\) mit
\( \quad f(x) = 0{,}4x^3 - 0{,}12x^2 - 0{,}18x + 0{,}2 \)
\(\\[2em]\)
Aufgabe 2 – 240 m über dem Meeresspiegel
Anhand des Querschnitts des Tals (Abbildung der Aufgabenstellung) können wir erkennen, dass es nur eine Stelle rechts vom Tiefpunkt gibt, für die diese Höhe \((f(x)=0{,}24)\)zutrifft. Wir berechnen diese Stelle mit
\( \quad \begin{array}{ r c l l } f(x) & = & 0{,}24 & \\[6pt] 0{,}4x^3 - 0{,}12x^2 - 0{,}18x + 0{,}2 & = & 0{,}24 &| \; - 0{,}24 \\[6pt] 0{,}4x^3 - 0{,}12x^2 - 0{,}18x - 0{,}04 & = & 0{,}24 & \\ \end{array} \)
\(\\\)
Mit der Taschenrechnerfunktion “Lösen einer Polynomfunktion” oder der SOLVE-Funktion erhalten wir den Wert
\( \quad x = 0.9129 \; {,} \)
also nach 912,9 m rechts vom Punkt \(A\) aus gesehen.
\(\\\)
Die Steigung an dieser Stelle, also die Steigung in einem Punkt, ist laut Tabelle
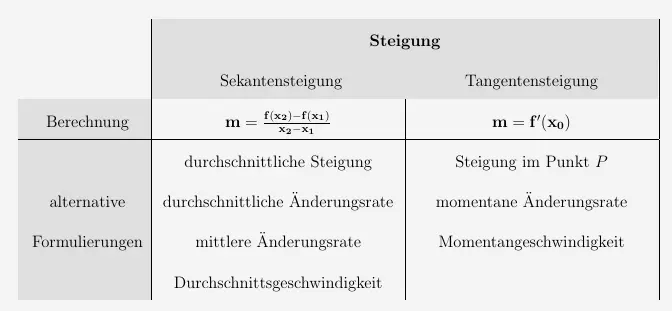
die 1. Ableitung der Funktion.
\(\\\)
Die Tangentensteigung wird nun berechnet mit \(f'(0{,}9129)\):
\( \quad \begin{array}{ r c l } f'(x) & = & 1{,}2x^2 - 0{,}24x - 0{,}18 \\[6pt] f'(0{,}9129) & = & 1{,}2 \cdot 0{,}9129^2 - 0{,}24 \cdot 0{,}9129 - 0{,}18 \\[6pt] f'(0{,}9129) & = & 0{,}6 \\ \end{array} \)
\(\\[2em]\)
Aufgabe 3 – Gefälle
Das durchschnittliche Gefälle wird nach der Tabelle aus der vorherigen Aufgabe berechnet mit
\( \quad m=\frac{f(x_2)-f(x_1)}{x_2-x_1} \)
\(\\\)
Mit Punkt \(A\) und Punkt \(T\) erhalten wir
\( \quad \begin{array}{ r c l } m & = & \frac{f(x_T)-f(x_A)}{x_T-x_A} \\[6pt] m & = & \frac{0{,}13-0{,}2}{0{,}5-0} \\[6pt] m & = & \frac{-0{,}07}{0{,}5} \\[6pt] m & = & -\frac{7}{50} \\[6pt] m & = & -0{,}14 \\ \end{array} \)
\(\\\)
Auf \(100 \; m\) in waagerechter Richtung geht es von Punkt \(A\) nach Punkt \(T\) durchschnittlich \(14 \; m\) abwärts.
Das maximale Gefälle haben wir in der Regel im Wendepunkt. Wir überprüfen, ob es für \(0 \leq x < 0{,}5\) einen Wendepunkt gibt.
Der Tiefpunkt kann natürlich kein Wendepunkt sein. Deshalb ist \(x=0{,}5\) aus der Überprüfung ausgenommen.
\(\\\)
notwendige Bedingung: \(f''(x) = 0\)
\(\\\) \( \quad \begin{array}{ r c l l } f''(x) & = & 2{,}4x - 0{,}24 & \\[6pt] 2{,}4x - 0{,}24 & = & 0 & | \; +0{,}24 \\[6pt] 2{,}4x & = & 0{,}24 & | \; : 2{,}4 \\[6pt] x & = & 0{,}1 & \\ \end{array} \)
\(\\\)
hinreichende Bedingung: \(f'''(x)\not= 0\)
\(\\\) \( \quad \begin{array}{ r c l l } f'''(x) & = & 2{,}4 & \\[6pt] f'''(0{,}1) & = & 2{,}4 \not= 0 & \quad \Rightarrow Wendepunkt \\ \end{array} \)
\(\\\)
Die Steigung im Wendepunkt ist
\( \quad \begin{array}{ r c l } f'(0{,}1) & = & 1{,}2 \cdot 0{,}1^2 - 0{,}24 \cdot 0{,}1- 0{,}18 \\[6pt] f'(0{,}1 & = & -0{,}192 \\ \end{array} \)
\(\\\)
Wir haben also ein maximales Gefälle von \(0{,}192\) . Das heißt, dass es auf \(100 \; m\) in horizontaler Richtung \(19{,}2 \; m\) abwärts geht.
\(\\\)