Ebene E
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Ebene in Koordinatenform
Die Koordinatenform der Ebene \(E\) ist von der Form
\( \quad E: \; ax_1 + bx_2 + cx_3 \; = \; d \)
\(\\\)
mit dem Normalenvektor \( \; \overrightarrow{n}= \begin{smallmatrix} \left( \begin{array}{r} a \\ b \\ c \end{array} \right) \end{smallmatrix} \).
\(\\\)
Den Normalenvektor bestimmen wir mit dem Kreuzprodukt der Richtungsvektoren
\( \quad \overrightarrow{AB} = \begin{smallmatrix} \left( \begin{array}{r} -22 \\ 0 \\ 28 \end{array} \right) \end{smallmatrix} \quad \text{und} \quad \overrightarrow{BC} = \begin{smallmatrix} \left( \begin{array}{r} 22 \\ -22 \\ 0 \end{array} \right) \end{smallmatrix} \)
\(\\\)
aus der vorherigen Aufgabe wie folgt:
\( \quad \begin{array}{ r c l} \overrightarrow{n} & = & \overrightarrow{AB} \times \overrightarrow{BC} \\[8pt] \overrightarrow{n} & =& \begin{smallmatrix} \left( \begin{array}{r} -22 \\ 0 \\ 28 \end{array} \right) \end{smallmatrix} \times \begin{smallmatrix} \left( \begin{array}{r} 22 \\ -22 \\ 0 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Dabei gehen wir folgendermaßen vor:
Die beiden Richtungsvektoren werden paarweise 2-mal untereinander geschrieben. Die erste und die letzte Zeile werden gestrichen. Dann wird über Kreuz multipliziert und jeweils die blaue Diagonale (Hauptdiagonale) minus die rote Diagonale (Nebendiagonale) gerechnet.

\(\\\)
Der Normalenvektor lautet \( \; \begin{smallmatrix} \left( \begin{array}{r} 616 \\ 616 \\ 484 \end{array} \right) \end{smallmatrix} \\ \)
In allen Werten stecken die Faktoren \(2 \cdot 22\). Wir können die Werte also durch \(44\) teilen. Dadurch ergibt sich ein anderer Vektor, der aber in die gleiche Richtung verläuft und auch ein Normalenvektor der Ebene \(E\) ist.
\( \quad \overrightarrow{n} \; = \; \begin{smallmatrix} \left( \begin{array}{r} 14 \\ 14 \\ 11 \end{array} \right) \end{smallmatrix} \\ \)
\(\\\)
Die vorläufige Koordinatengleichung lautet nun
\( \quad 14x_1 + 14x_2 + 11x_3 \; = \; d \)
\(\\\)
Um \(d\) zu bestimmen, setzen wir Punkt \(A(11|11|0)\) ein.
\( \quad \begin{array}{ r c l l } 14 \cdot 11 + 14 \cdot 11 + 11 \cdot 0 & = & d \\[8pt] 308 & = & d \\ \end{array} \)
\(\\\)
Die Koordinatenform von \(E\) lautet also
\( \quad 14x_1 + 14x_2 + 11x_3 \; = \; 308 \)
\(\\[2em]\)
Aufgabe 2 – Abstand d
Wert von d
Den Abstand eines Punktes von einer Ebene berechnen wir mit Hesse’schen Normalenform.
\( \quad HNF: \; ( \overrightarrow{x} - \overrightarrow{p}) \cdot \overrightarrow{n_0} \; = \; 0 \)
\(\\\)
Für die Hesse’schen Normalenform benötigen wir den Einheitsvektor des Normalenvektors \(\overrightarrow{n}\) mit
\( \quad \overrightarrow{n_0} \; = \; \dfrac{\overrightarrow{n}}{|\overrightarrow{n}|}, \)
\(\\\)
wobei \(\; \overrightarrow{n} = \begin{smallmatrix} \left( \begin{array}{r} a \\ b \\ c \end{array} \right) \end{smallmatrix} \;\) und \(\; |\overrightarrow{n}| = \sqrt{a^2 + b^2 + c^2} \;\) ist.
\(\\\)
Beides ist in der Schreibweise für die Koordinatenform
\( \quad HNF: \; \dfrac{\bigl|a \cdot x_1 + b \cdot x_2 + c \cdot x_3 - d\bigl|}{\sqrt{a^2 + b^2 + c^2}} \; = \; 0 \)
\(\\\)
bereits enthalten. Wir setzen nun Punkt \(D\) in die Koordinatenform der Ebene \(E\) ein, lassen \(= 0\) weg und berechnen den Abstand.
\( \quad \begin{array}{ r c l } Abst(D,E) & = & \dfrac{| 14 \cdot (-11) + 14 \cdot (-11) + 11 \cdot 0 - 308 |}{\sqrt{14^2 + 14^2 + 11^2}} \\[8pt] & = & \dfrac{| -616 |}{\sqrt{513}} \\[8pt] & \approx & 27{,}2 \, LE \\ \end{array} \)
\(\\[2em]\)
Volumen der Pyramide

Der Term
\( \quad \dfrac{d}{6} \cdot \bigl|\overrightarrow{AB} \times \overrightarrow{BC}\bigl| \)
\(\\\)
drückt aus, dass die Pyramide exakt dreimal in den Quader passt. Im Einzelnen:
\(\\\)
Der Term
\( \quad \bigl|\overrightarrow{AB} \times \overrightarrow{BC}\bigl| \)
\(\\\)
berechnet die Fläche des Parallelogramms, das durch diese beiden Vektoren aufgespannt wird.

\(\\\) Gezeichnet sind hier der Anschaulichkeit halber die Vektoren \(\overrightarrow{BA}\) und \(\overrightarrow{BC}\) mit dem zugehörigen Parallelogramm, das in diesem Fall flächengleich zu dem des Terms ist.
Es ist hier gut zu erkennen, dass das Dreieck \(ABC\) genau halb so groß ist wie das Parallelogramm. Deshalb gilt für die Dreiecksfläche, die zugleich die Grundfläche \(G\) der Pyramide ist,
\( \quad G \; = \; \frac{1}{2} \cdot \bigl|\overrightarrow{AB} \times \overrightarrow{BC}\bigl| \)
\(\\\)
Der berechnete Wert von \(d\) gibt die Höhe der Pyramide an.
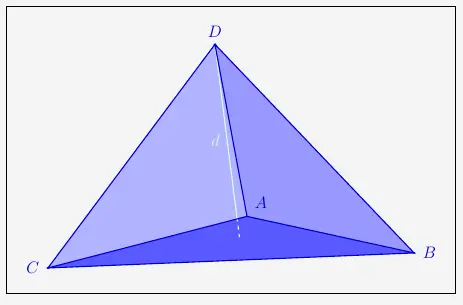
Mit der Volumenformel einer Pyramide folgt
\( \quad \begin{array}{ r c l } V & = & \frac{1}{3} \cdot G \cdot h \\[8pt] & = & \frac{1}{3} \cdot \frac{1}{2} \cdot \bigl|\overrightarrow{AB} \times \overrightarrow{BC}\bigl| \cdot h \\[8pt] & = & \frac{1}{6} \cdot \bigl|\overrightarrow{AB} \times \overrightarrow{BC}\bigl| \cdot h \\[8pt] & = & \frac{h}{6} \cdot \bigl|\overrightarrow{AB} \times \overrightarrow{BC}\bigl| \\ \end{array} \)
\(\\[2em]\)
Aufgabe 3 – Winkel der Ebene
Den Schnittwinkel der Ebene \(E\) mit der \(x_1x_2\)-Ebene berechnen wir mit
\( \quad cos(\alpha) = \displaystyle{ \frac{ \bigl| \overrightarrow{n_1} \circ \overrightarrow{n_2} \bigl| } { \bigl| \overrightarrow{n_1} \bigl| \cdot \bigl| \overrightarrow{n_2} \bigl| } } \)
\(\\\)
Wir verwenden dabei
\( \quad \overrightarrow{n_1}= \begin{smallmatrix} \left( \begin{array}{r} 14 \\ 14 \\ 11 \end{array} \right) \end{smallmatrix} \)
\(\\\)
und für die \(x_1x_2\)-Ebene einen Vektor,

der orthogonal zu dieser Ebene ist, zum Beispiel den Vektor
\( \quad \overrightarrow{n_2}= \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} \)
\(\\\)Für den gesuchten Winkel gilt
\( \quad \begin{array}{ r c l } \displaystyle{cos(\alpha)} & = & \frac{ \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 14 \\ 14 \\ 11 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} \end{vmatrix} } { \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 14 \\ 14 \\ 11 \end{array} \right) \end{smallmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} \end{vmatrix} } \\[10pt] \displaystyle{cos(\alpha)} & = & \dfrac{\bigl| 14 \cdot 0 + 14 \cdot 0 + 11 \cdot 1 \bigl| } { \displaystyle{ \sqrt{ 14^2 +14^2 + 11^2 } } \cdot \displaystyle{ \sqrt{ 0^2 +0^2 + 1^2 } } } \\[10pt] \displaystyle{cos(\alpha)} & = & \dfrac{ 11 } { \displaystyle{ \sqrt{ 513 } \cdot \sqrt{ 1 } } } \\[10pt] \displaystyle{\alpha} & = & cos^{-1}\left(\dfrac{ 11 } { \displaystyle{ \sqrt{ 513 } } } \right) \; = \; 60{,}94^\circ \\ \end{array} \)
\(\\\)