HMF 5
Analytische Geometrie (Pool 1)
Gegeben ist die Ebene \(E\) mit
\(\quad E : x_1 + 3x_2 + 2x_3 = 6 \)
Die Schnittpunkte der Ebene \(E\) mit den Koordinatenachsen sind die sogenannten Spurpunkte der Ebene \(E\). So ist \(S_1(6|0|0)\) ein Spurpunkt der Ebene \(E\).
\(\\\)
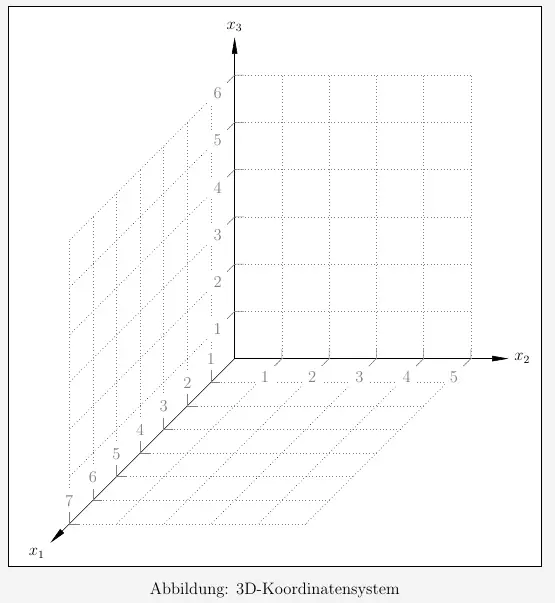
\(\qquad \qquad \qquad \quad\)
\(\\\)
Aufgabe 1
Geben Sie die Koordinaten der anderen beiden Spurpunkte \(S_2\) und \(S_3\) der Ebene \(E\) an und zeichnen Sie das Dreieck \(S_1S_2S_3\) in das Koordinatensystem ein.
(3 P)
\(\\\)
Aufgabe 2
Es gibt unendlich viele Geraden, die parallel zu \(E\) sind und durch den Punkt \(P(2|5|7)\) verlaufen.
Bestimmen Sie eine Gleichung einer solchen Geraden \(g\).
(2 P)
\(\\[2em]\)