Rechnen mit Vektoren
Inhaltsverzeichnis
\(\\\)
Im Gegensatz zum Rechnen mit reellen Zahlen ist Division nicht definiert und nicht erlaubt.
\(\\[1em]\)
Vektoraddition und Vektorsubtraktion
Vektoren können miteinander addiert werden, sofern sie von gleicher Dimension sind, jedoch nicht mit Skalaren. Das heißt, dass zum Beispiel die Rechnungen
\( 3 + \begin{smallmatrix} \left( \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right) \end{smallmatrix} \) und \( \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 3 \end{array} \right) \end{smallmatrix} + \begin{smallmatrix} \left( \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right) \end{smallmatrix} \)
nicht definiert sind.
\(\\\)
Geometrisch ist eine Vektoraddition eine Vektorkette von hintereinander liegenden Vektoren.
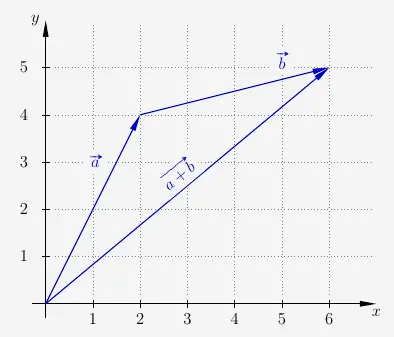
Entsprechend ist eine Vektorsubtraktion eine Vektorkette mit dem Gegenvektor.
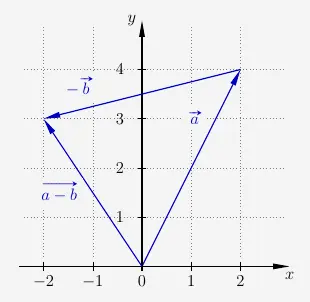
Eine Vektoraddition wird auf folgende Weise durchgeführt.
\(\\\)
Vektoraddition in der Ebene
\( \begin{array}{ l*{5}{l} } \vec{a} + \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \end{smallmatrix} +\begin{smallmatrix} \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 + b_1 \\ a_2 + b_2 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\\)
Vektoraddition im Raum
\( \begin{array}{ l*{5}{l} } \vec{a} + \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \end{smallmatrix} +\begin{smallmatrix} \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 + b_1 \\ a_2 + b_2 \\ a_3 + b_3 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\[1em]\)
Entsprechend die Vektorsubtraktion.
\(\\\)
Vektorsubtraktion in der Ebene
\( \begin{array}{ l*{5}{l} } \vec{a} - \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 - b_1 \\ a_2 - b_2 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\\)
Vektorsubtraktion im Raum
\( \begin{array}{ l*{5}{l} } \vec{a} - \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 - b_1 \\ a_2 - b_2 \\ a_3 - b_3 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\[1em]\)
Die Rechnungen der obigen Darstellungen lauten dann
\( \quad \begin{array}{ l*{7}{l} } \vec{a} + \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 4 \end{array} \right) \end{smallmatrix} +\begin{smallmatrix} \left( \begin{array}{c} 4 \\ 1 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 + 4 \\ 4 + 1 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 6 \\ 5 \end{array} \right) \end{smallmatrix} \end{array} \)
und
\( \quad \begin{array}{ l*{9}{l} } \vec{a} - \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 4 \end{array} \right) \end{smallmatrix} + \begin{smallmatrix} \left( \begin{array}{c} -4 \\ -1 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 + (-4) \\ 4 + (-1) \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 - 4 \\ 4 - 1 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 3 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\[2em]\)
Multiplikation von Vektoren
Die eine Multiplikation gibt es nicht. Vielmehr werden 3 verschiedene Arten von Multiplikationen unterschieden.
\(\\\)
S-Multiplikation
Die S-Multiplikation ist eine Multiplikation zwischen einem Vektor und einem Skalar. Was bei der Addition nicht erlaubt ist, Berechnung mit Skalar und Vektor, geht bei der Multiplikation schon. Die S-Multiplikation wird nun gebildet
bei Vektoren in der Ebene mit
\( \begin{array}{ l*{5}{l} } c \cdot \vec{a} & = & c \cdot \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} c \cdot a_1 \\ c \cdot a_2 \end{array} \right) \end{smallmatrix} \end{array} \)
und bei Vektoren im Raum mit
\( \begin{array}{ l*{5}{l} } c \cdot \vec{a} & = & c \cdot \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} c \cdot a_1 \\ c \cdot a_2 \\ c \cdot a_3 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\\)
Geometrisch kann eine S-Multiplikation veranschaulicht werden mit
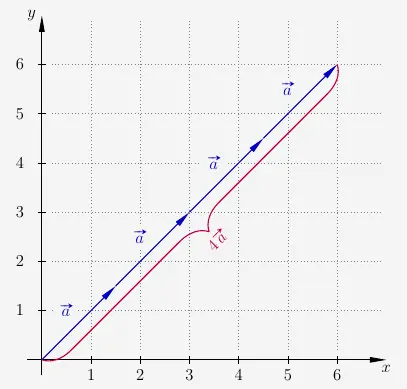
\(\\[2em]\)
Multiplikationen mit 2 Vektoren
Diese Multiplikationen sind benannt nach ihrem Ergebnis:
- Skalarprodukt (das Ergebnis ist ein Skalar)
- Vektorprodukt (das Ergebnis ist ein Vektor), das Vektorprodukt heißt auch Kreuzprodukt gemäß seiner Schreibweise
\(\\\)
Skalarprodukt
Das Skalarprodukt kann mit verschiedenen Zeichen geschrieben werden.
Üblich sind: \(\cdot\), \(\circ\), \(\ast\), •
Im Studium in der Disziplin ,,Lineare Algebra’‘ wird der Mal-Punkt verwendet. Ich bevorzuge und verwende jedoch das Zeichen \(\circ\), um Verwechselungen mit der S-Multiplikation zu vermeiden.
\(\\\)
Das Skalarprodukt wird gebildet bei Vektoren in der Ebene mit
\( \begin{array}{ l*{5}{l} } \vec{a} \circ \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) \end{smallmatrix} & = & a_1 \cdot b_1 \; + \; a_2 \cdot b_2 \end{array} \)
\(\\\)
und bei Vektoren im Raum mit
\( \begin{array}{ l*{5}{l} } \vec{a} \circ \vec{b} & = & \begin{smallmatrix} \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) \end{smallmatrix} & = & a_1 \cdot b_1 \; + \; a_2 \cdot b_2 \; + \; a_3 \cdot b_3 \end{array} \)
\(\\[2em]\)
Orthogonalität von Vektoren
Sind zwei Vektoren \(\vec{a}\) und \(\vec{b}\) orthogonal zueinander, das heißt, dass sie einen 90°-Winkel miteinander bilden, so gilt die Gleichung
\( \vec{a} \circ \vec{b} \; = \; 0 \)
\(\\\)
Sind ferner zwei linear unabhängige Vektoren \(\vec{a}\) und \(\vec{b}\) jeweils orthogonal zu einem dritten Vektor \(\vec{n}\), so ist dieser Vektor der Normalenvektor bezüglich der Vektoren \(\vec{a}\) und \(\vec{b}\). Es gilt dann
\( \vec{a} \circ \vec{n} \; = \; 0 \qquad \textit{und} \qquad \vec{b} \circ \vec{n} \; = \; 0 \)
\(\\[2em]\)
Kreuzprodukt
Das Kreuzprodukt oder auch Vektorprodukt zweier Vektoren wird mithilfe der Berechnung von Determinanten einer Matrix ermittelt. Was ist nun eine Matrix und ihre Determinante?
Eine Matrix ist eine Anordnung von Elementen, in der Regel Zahlen oder Variablen, die in Zeilen und Spalten vorliegen, ähnlich wie bei einer Tabelle. Als Beispiel folgt eine \((2 \times 2)\) – Matrix, also mit 2 Zeilen und 2 Spalten.
\( \quad \begin{array}{ r c l } \mathbf{M} &= & \begin{pmatrix} a & c \\ b & d \\ \end{pmatrix} \end{array} \)
\(\\\)
Ein Vektor kann, zumindest von der Schreibweise her, als eine einspaltige Matrix verstanden werden. Allerdings unterscheiden sich Matrizen und Vektoren in ihren Eigenschaften.
Die Determinante dieser Matrix wird nun folgendermaßen geschrieben und berechnet:
\( \quad \begin{array}{ r c l c l } det \; \mathbf{M} &= & \begin{vmatrix} a & c \\ b & d \\ \end{vmatrix} & = & a \cdot d - b \cdot c \\ \end{array} \)
\(\\\)
Diese Berechnungsweise kommt im Kreuzprodukt zur Anwendung.
Bis hierhin soll es nun zu Matrizen und Determinanten genügen. Zu einem späteren Zeitpunkt werden diese Themen in Extrabeiträgen ausführlich behandelt.
\(\\[2em]\)
Normalenvektor
Wie bei der vorherigen Aufgabe zu sehen war, lässt sich der Normalenvektor mit zwei Skalarprodukten berechnen. Einfacher noch geht es mit dem Kreuzprodukt.
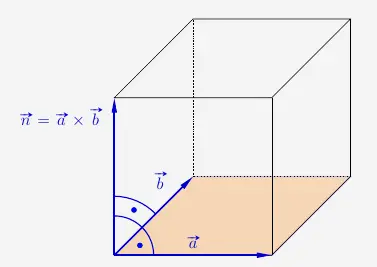
Ist ein Vektor \(\vec{n}\) der Normalenvektor von den Vektoren \(\vec{a}\) und \(\vec{b}\), also orthogonal zu diesen beiden, so kann \(\vec{n}\) mit dem Kreuzprodukt von \(\vec{a}\) und \(\vec{b}\) berechnet werden.
\(\\\)
Seien nun
\( \quad \vec{a} = \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 2 \\ -1 \end{array} \right) \end{smallmatrix} \) und \( \vec{b} = \begin{smallmatrix} \left( \begin{array}{r} 2 \\ 3 \\ 0 \end{array} \right) \end{smallmatrix} \)
\(\\\)
Dann ist
\( \quad \vec{n} = \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 2 \\ -1 \end{array} \right) \end{smallmatrix} \times \begin{smallmatrix} \left( \begin{array}{r} 2 \\ 3 \\ 0 \end{array} \right) \end{smallmatrix} \)
\(\\\)
Die Berechnung geht nun wie folgt vonstatten: Die Vektoren \(\vec{a}\) und \(\vec{b}\) werden jeweils zweimal untereinander geschrieben und nebeneinander gestellt. Es entsteht quasi eine \((6 \times 2)\) – Matrix. Die erste und die letzte Zeile davon werden gestrichen. Jeweils 2 der verbliebenen Zeilen werden zu Matrizen wie dargestellt zusammengefasst und deren Determinante berechnet.

\(\\\)
Aus den Ergebnisse bildet sich der Normalenvektor mit
\( \quad \vec{n} = \begin{smallmatrix} \left( \begin{array}{r} 3 \\ -2 \\ 8 \end{array} \right) \end{smallmatrix} \)
\(\\[2em]\)
Flächenberechnung mit Vektoren
Die Fläche eines Parallelogramms
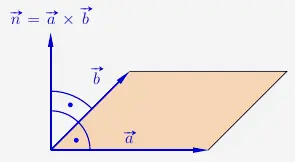
wird berechnet mit dem Betrag des Kreuzproduktes der Vektoren, die dieses Parallelogramm aufspannen.
\( \quad \begin{array}{ r c l } A & = & \begin{vmatrix} \vec{a} \times \vec{b} \\ \end{vmatrix} \\ \end{array} \)
Die Fläche entspricht also dem Betrag des Normalenvektors der Spannvektoren.
\(\\\)
Die Fläche eines Dreiecks
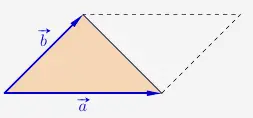
entspricht der Fläche des halben Parallelogramms.
\( \quad \begin{array}{ r c l } A & = & \frac{1}{2} \cdot \begin{vmatrix} \vec{a} \times \vec{b} \\ \end{vmatrix} \\ \end{array} \)
\(\\\)
Eine andere Möglichkeit die Fläche eines Dreiecks zu berechnen besteht darin, die Beträge zweier Spannvektor und deren eingeschlossenen Winkel zu verwenden.
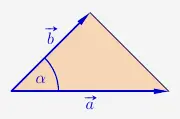
\( \quad \begin{array}{ r c l } A & = & \frac{1}{2} \cdot |\vec{a}| \cdot |\vec{b}| \cdot sin(\alpha) \\ \end{array} \)
\(\\\)
Da die Berechnung des Winkels aber relativ aufwändig ist, kommt dieses Verfahren eher selten zur Anwendung.