Spiegeln von Funktionen
Inhaltsverzeichnis
\(\\\)
1. Achsenspiegelung
Eine Funktion kann sowohl um die \(x\)-Achse als auch um die \(y\)-Achse gespiegelt werden.
Der Graph einer Funktion \(f\) mit der Funktionsvorschrift \(f(x)\) wird durch
\(\quad f(-x) \)
\(\\\) um die \(y\)-Achse gespiegelt und durch
\(\quad -f(x) \)
\(\\\) um die \(x\)-Achse gespiegelt.
\(\\\)
Es folgen Beispiele zu exponentielle Funktionen (incl. e-Funktion), Logarithmusfunktionen, trigonometrischen Funktionen und ganzrationalen Funktionen.
\(\\[2em]\)
2. Spiegelung von exponentiellen Funktionen
Spiegelung um die y-Achse von exponentiellen Funktionen
Eine Funktion \(e^x\) wird laut Achsenspiegelung mit \(e^{-x}\) um die \(y\)-Achse gespiegelt.
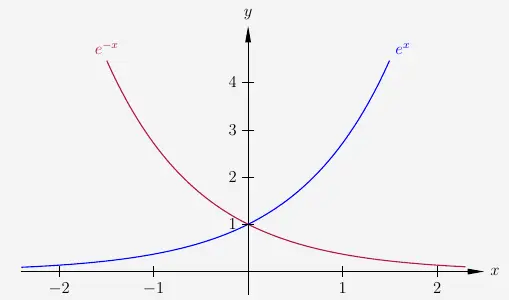
\(\\\)
Bei Exponentialfunktionen von der Form \(b^x\) mit \(b \not= e\) ist nun mit \(\left(\frac{1}{b}\right)^x\) gespiegelt worden.
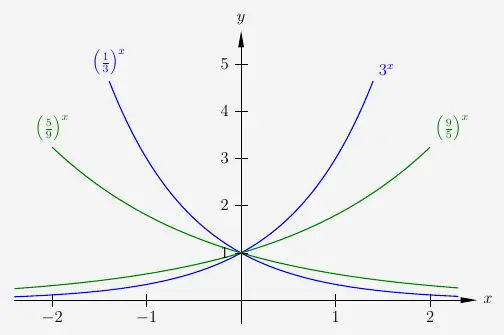
\(\\\)
Was bedeutet das?
Formen wir jetzt den Ausdruck \(\left(\frac{1}{b}\right)^x\) mit dem 2. Potenzgesetz um, so erhalten wir Folgendes:
\( \quad \begin{array}{ r c l } \left(\frac{1}{b}\right)^x & = & \frac{1^x}{b^x} \\ \end{array} \)
\(\\\) Mit
\(\quad \underbrace{1 \cdot 1 \cdot 1 \cdot 1 \dots 1}_{\substack{x-mal}} \; = \; 1 \)
\(\\\) und der Potenzregel für negative Potenzen folgt
\( \quad \frac{1^x}{b^x} \; = \; \frac{1}{b^x} \; = \; b^{-x} \)
\(\\\)
Im Grunde ist also \(\left(\frac{1}{b}\right)^x\) das Gleiche wie \(b^{-x}\) . Es gilt auch hier für die Spiegelung \(f(-x)\). Jedoch ist bei Exponentialfunktionen die Schreibweise
\(\quad \left(\frac{1}{b}\right)^x \)
üblich.
\(\\[2em]\)
Spiegelung um die x-Achse von exponentiellen Funktionen
Bei der Spiegelung um die \(x\)-Achse bekommen die gespiegelte \(e\)-Funktion
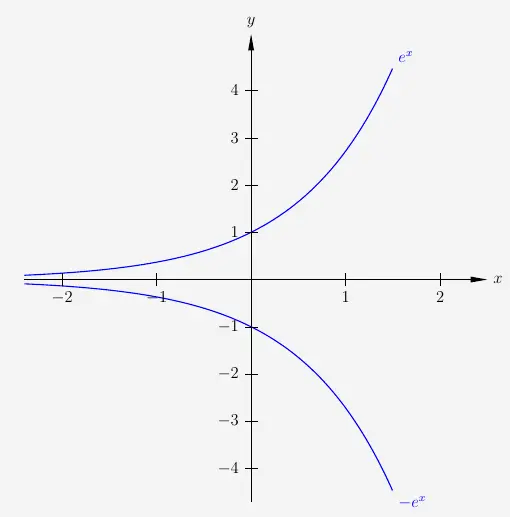
\(\\\)
und die gespiegelte exponentielle Funktion
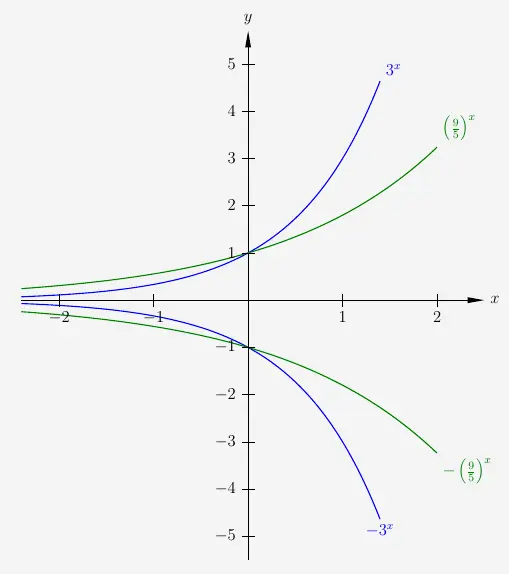
\(\\\)
ein Minus vor dem Funktionsterm.
\(\\[2em]\)
3. Spiegelung von ganzrationalen Funktionen
Spiegelung um die y-Achse von ganzrationalen Funktionen
Hier wird bei der Spiegelung der \(x\)-Wert negativ.
\(\\\)
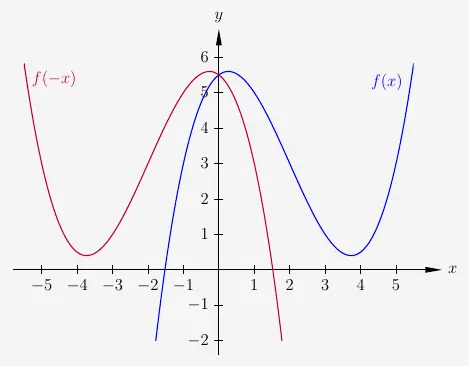
\(\\\) Es ergeben sich also die Ausdrücke
\( \quad \begin{array}{ r c c c c c c c l } f(x) & = & 0{,}25x^3 & - & 1{,}5x^2 & + & 0{,}75x & + & 5{,}5 \\[6pt] f(-x) & = & 0{,}25 \cdot (-x)^3 & - & 1{,}5 \cdot (-x)^2 & + & 0{,}75 \cdot (-x) & + & 5{,}5 \\ \end{array} \)
\(\\[2em]\)
Spiegelung um die x-Achse von ganzrationalen Funktionen
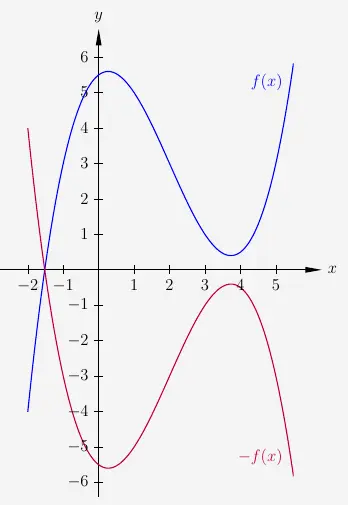
\( \quad \begin{array}{ r c c } f(x) & = & 0{,}25x^3 \; - \; 1{,}5x^2 \; + \; 0{,}75x \; + \; 5{,}5 \\[15pt] -f(x) & = & - \left(0{,}25x^3 \; - \; 1{,}5x^2 \; + \; 0{,}75x \; + \; 5{,}5 \right) \\[6pt] & = & - \; 0{,}25x^3 \; + \; 1{,}5x^2 \; - \; 0{,}75x \; - \; 5{,}5 \\ \end{array} \)
\(\\[2em]\)
Spiegelungen von verschobenen ganzrationalen Funktionen
Entsprechend verhält es sich, wenn eine verschobene ganzrationale Funktion vorliegt.
Wir betrachten die Spiegelung um die \(y\)-Achse
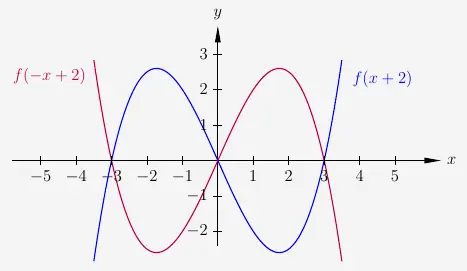
und die Spiegelung um die \(x\)-Achse.
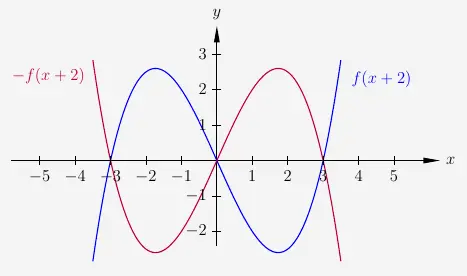
Offensichtlich entstehen in diesem Fall dieselben Graphen. Hier scheint es sich um eine punktsymmetrische Funktion \(f\) zu handeln; vergleiche Punktsymmetrie.
\(\\\) Aber vorerst zurück zu den obigen Spiegelungen. Wir erhalten folgende Funktionsterme:
\(\quad \begin{array}{ r c r c l c l c l } f(x+2) & = & 0{,}25(x+2)^3 & - & 1{,}5(x+2)^2 & + & 0{,}75(x+2) & + & 2{,}5 \\[8pt] f(-x+2) & = & 0{,}25(-x+2)^3 & - & 1{,}5(-x+2)^2 & + & 0{,}75(-x+2) & + & 2{,}5 \\[24pt] f(x+2) & = & 0{,}25(x+2)^3 & - & 1{,}5(x+2)^2 & + & 0{,}75(x+2) & + & 2{,}5 \\[8pt] -f(x+2) & = & - \; \left( \; 0{,}25(x+2)^3 \right. & - & 1{,}5 (x+2)^2 & + & 0{,}75 (x+2) & + & \left. 2{,}5 \; \right) \\ \end{array} \)
\(\\[2em]\)
4. Spiegelung von trigonometrischen Funktionen
Spiegelung um die y-Achse von trigonometrischen Funktionen
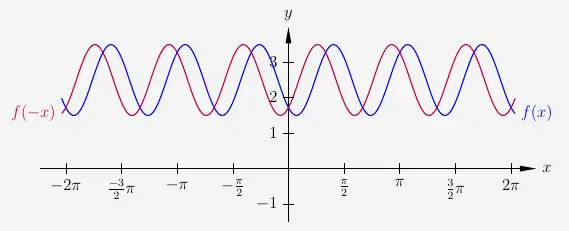
mit
\( \quad \begin{array}{ r c l } f(x) & = & 3sin(x - 0{,}75)+2{,}5 \\[6pt] f(-x) & = & 3sin(- x - 0{,}75)+2{,}5 \\ \end{array} \)
\(\\[2em]\)
Spiegelung um die x-Achse von trigonometrischen Funktionen
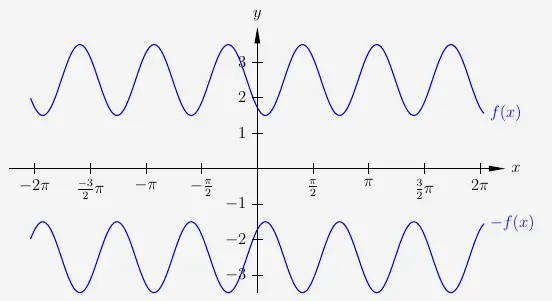
mit
\( \quad \begin{array}{ r c l } f(x) & = & 3sin(x - 0{,}75)+2{,}5 \\[15pt] -f(x) & = & - \Big(3sin(x - 0{,}75) + 2{,}5\Big) \\[6pt] & = & - 3sin(x - 0{,}75) - 2{,}5 \\ \end{array} \)
\(\\[2em]\)
5. Spiegelung von Logarithmusfunktionen
Spiegelung um die y-Achse von Logarithmusfunktionen
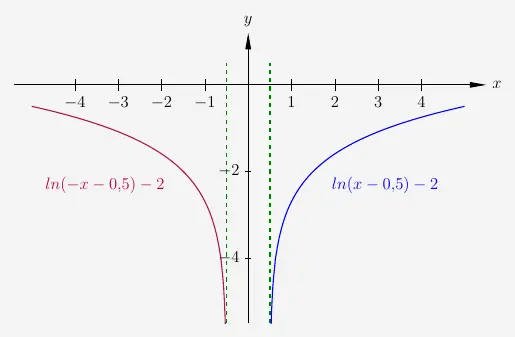
Beachte:
Der Logarithmus kann nur aus positiven Zahlen gezogen werden.
\(\\\)
Also gilt
\( \quad \begin{array}{ r c l c l } f(x) & = & ln(x-0{,5})-2 & \textrm{mit} & x > 0{,}5 \\[6pt] f(-x) & = & ln(-x-0{,5})-2 & \textrm{mit} & x < -0{,}5 \\ \end{array} \)
\(\\[2em]\)
Spiegelung um die x-Achse von Logarithmusfunktionen
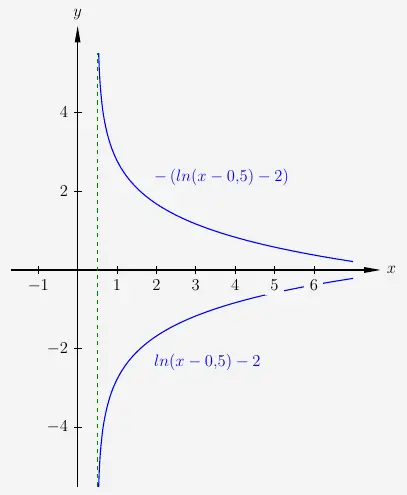
Es gilt
\( \quad \begin{array}{ r c c c l } f(x) & = & ln(x-0{,5})-2 & \textrm{mit} & x > 0{,}5 \\[6pt] -f(x) & = & - \left( ln(x-0{,5}) - 2 \right) & \textrm{mit} & x > 0{,}5 \\ \end{array} \)
\(\\[1em]\)