Streckung von Funktionen
Inhaltsverzeichnis
\(\\\)
Das Strecken und Stauchen von Funktion kann am besten anhand von trigonometrischen Funktionen deutlich gemacht werden.
\(\\\)
1. Streckung und Stauchung von trigonometrischen Funktionen
Streckung und Stauchung in y-Richtung

Zieht man eine Kugel, die an einer Feder hängt, nach unten und lässt sie los, so beginnt die Feder zu schwingen. In zeitlicher Abfolge nimmt die Kugel Positionen gemäß einer Sinuskurve ein. Die Auslenkung aus der Ruhelage der Feder nennt man Amplitude.

Die Amplitude gibt die Streckung der Funktion
\( \quad f(x) \; = \; sin(x) \)
durch
\( \quad f(x) \; = \; a \cdot sin(x) \)
\(\\\)
in \(y\)-Richtung mit dem Parameter \(a\) an. Dabei gilt:
a > 1 : Streckung der Sinusfunktion
a < 1 : Stauchung der Sinusfunktion
Negative \(a\)-Werte ergeben eine Spiegelung um die \(x\)-Achse.
\(\\[2em]\)
Streckung und Stauchung in x-Richtung
Bei der allgemeinen Gleichung der trigonometrischen Funktionen
\(\quad f(x) \; = \; a \cdot sin \big( b \cdot (x - c) \big) + d \)
\(\\\)
ist der Parameter \(b\) verantwortlich für die Streckung/Stauchung in \(x\)-Richtung.
Nach einer Schwingung der Feder im obigen Modell kehren die Funktionswerte periodisch wieder. Wir sprechen bei den trigonometrischen Funktionen von periodischen Funktionen.

Bei der Funktion von \(sin(x)\) hat eine Periode die Länge von \(2 \pi\) .
Das bedeutet, dass der Parameter \(b\) gleichzeitig die Frequenz, also wie häufig eine Periode auf \(2 \pi\) vorkommt.

Beim roten Graphen sind also 3 komplette Schwingungen auf der Länge von \(2 \pi\) enthalten.
\(\\[2em]\)
2. Streckung und Stauchung von exponentiellen Funktionen
Streckung und Stauchung in \(x\)-Richtung von exponentiellen Funktionen
Bei Funktion vom Typ \(b^x\) wird die Streckung (Stauchung) in \(x\)-Richtung durch die Basis \(b\) der Potenz gesteuert.
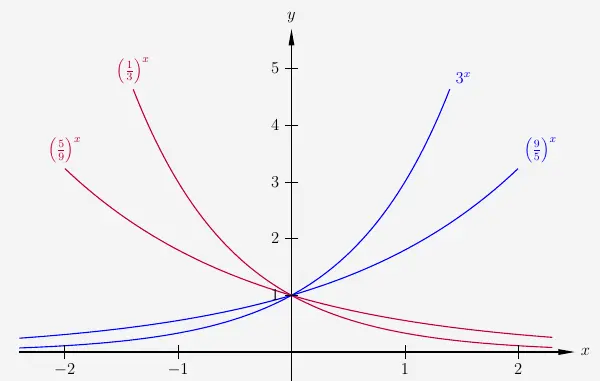
Dabei bewirkt
b > 1 eine Stauchung des Graphen der Funktion in \(x\)-Richtung
b < 1 eine Streckung des Graphen der Funktion in \(x\)-Richtung
\(\\\)
Es gilt, dass \(b\) stets positiv ist und alle Graphen durch den Punkt \((0 | 1)\) laufen.
\(\\[2em]\)
Streckung und Stauchung in \(y\)-Richtung von exponentiellen Funktionen
Die Streckung (Stauchung) in \(y\)-Richtung in der Form
\( \quad f(x) \; = \; a \cdot b^x \)
\(\\\)
wird durch den Parameter \(a\) bestimmt. Jeder Graph schneidet die \(y\)-Achse bei \((0 | a)\).
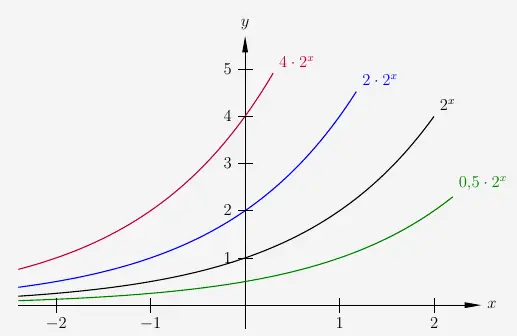
Negative \(a\)-Werte bewirken eine Spiegelung des Graphen um die \(x\)-Achse.
\(\\[2em]\)
3. Streckung und Stauchung von e-Funktionen
Streckung und Stauchung in \(x\)-Richtung von e-Funktionen
Die Streckung und Stauchung in \(x\)-Richtung einer \(e\)-Funktion entspricht im Prinzip der einer exponentiellen Funktion. Nur ist die Basis jetzt schon belegt mit \(e\). Wir müssen also \(b^x\) umschreiben in \(e^{k \cdot x}\).
Dies können wir durch die Umkehrung \(ln(x)\) des Ausdrucks \(e^x\) erreichen, denn es gilt die Beziehung :
\( \quad \displaystyle{b^x \; = \; e^{ln(b) \cdot x}} \)
Wir verwenden also
\(\quad f(x) \; = \; e^{k \cdot x} \quad \text{mit} \quad k = ln(b) \)

Für wachsende \(e\)-Funktionen ist \(k > 0\). Dabei bewirkt
- b > 1 eine Stauchung des Graphen der Funktion in \(x\)-Richtung
- b < 1 eine Streckung des Graphen der Funktion in \(x\)-Richtung
Negative \(k\)-Werte bewirken eine Spiegelung des Graphen um die \(y\)-Achse.
\(\\[2em]\)
Streckung und Stauchung in \(y\)-Richtung von e-Funktionen
Eine Streckung/Stauchung in \(y\)-Richtung einer \(e\)-Funktion erfolgt entsprechend der exponentiellen Funktionen mit
\( \quad f(x) \; = \; a \cdot e^x \)
\(\\\)

Auch hier gilt, dass der Streckungsfaktor \(a\) gleichzeitig der Schnittpunkt mit der \(y\)-Achse ist.
\(\\[2em]\)
4. Streckung und Stauchung von ganzrationalen Funktionen
Im Gegensatz zu den anderen Funktionstypen ist es hier üblich, nur in \(y\)-Richtung zu strecken oder zu stauchen. Bei ganzrationalen Funktionen in der Form
\( \quad f(x) \; = \; ax^n \; + \; bx^{n-1} \; + \; cx^{n-2} \; + \; dx^{n-3} \; + \; \dots \)
\(\\\)
bildet der Parameter \(a\) den Streckungsfaktor. Eine Ausnahme stellt das Polynom
\( \quad f(x) \; = \; ax \; + \; b \)
\(\\\)
dar. Hier handelt es sich um eine lineare Funktion, die wie folgt notiert wird :
\( \quad f(x) \; = \; mx \; + \; b \)
\(\\\)
\(m\) bezeichnet dabei die Steigung der Funktion, die durch eine Gerade darstellt wird.
Als Beispiel der Streckung und Stauchung von Polynomen betrachten wir die Potenzfunktion
\( \quad f(x) \; = \; ax^2 \)
\(\\\)

Es gilt
a < 1 bewirkt eine Stauchung der Normalparabel
a > 1 bewirkt eine Streckung der Normalparabel
Negative \(a\)-Werte bewirken eine Spiegelung des Graphen um die \(x\)-Achse.
\(\\[1em]\)