Boxplot (Casio fx-991DE X)

---

Für den Boxplot nehmen wir folgendes Beispiel:

In einem Supermarkt wird die Verweildauer von 60 Kunden in ganzen Minuten gemessen.

\(\\\)

Dafür muss die entsprechende Tabelle so eingestellt werden, dass die Häufigkeiten von \(x\)-Werten eingegeben werden können.

Wir gehen dazu in das SETUP-Menu mit \(\boxed{\color{#C19A6B}{SHIFT}}\) \(\boxed{MENU}\)

\(\\\)

Mit

\(\\\)

bekommen wir

\(\\\)

\(\boxed{3}\) auswählen

\(\\\)

und \(\boxed{1}\) auswählen.

Nun gehen wir in den Statistikbereich unter dem \(\boxed{MENU}\). Wir gehen nach rechts mit den Pfeiltasten

\(\\\)

bis

\(\\\)

erscheint und bestätigen mit \(\boxed{=}\).

\(\\\)

Wir wählen \(\boxed{1}\)

\(\\\)

Wir befüllen die Tabelle mit den obigen Tabellenwerten und haben dann folgende Anzeige:

\(\\\)

Zur Auswertung betätigen wir \(\boxed{OPTN}\)

\(\\\)

und wählen \(\boxed{3}\) und erhalten eine Reihe von Werten:

\(\\\)

Weitere Werte sehen wir mit

\(\\\)

und noch einmal

\(\\\)

Uns interessieren nur folgende Daten:

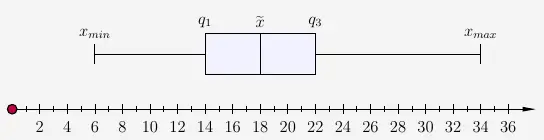
\( \begin{array}{ l r c r } \textrm{Kunden insgesamt :} & \quad n & = & 60 \\[6pt] \textrm{Untergrenze der Minuten :} & \quad min(x) & = & 6 \\[6pt] \textrm{1. Quartil (25%) :} & \quad Q_1 & = & 14 \\[6pt] \textrm{Median (50%) :} & \quad Med & = & 18 \\[6pt] \textrm{3. Quartil (75%) :} & \quad Q_3 & = & 22 \\[6pt] \textrm{Obergrenze der Minuten :} & \quad max(x) & = & 34 \\ \end{array} \)

\(\\[1em]\)

Daraus lässt sich nun der folgende Boxplot zeichnen:

\(\\[1em]\)