Horner-Schema
Das Horner-Schema arbeitet wie auch die Polynomdivision mit dem Abspalten eines Linearfaktors. Das Horner-Schema ist aber wesentlich übersichtlicher und damit auch nicht so anfällig für Fehler.
Wir lösen die Gleichung
\( \quad 0 = 2x^3 - 18 x^2 + 28x + 4 \)
\(\\\)
Die ersten Schritte sind mit denen der Polynomdivision identisch. Wir bestimmen die 1. Nullstelle mit einer Wertetabelle. Wir geben in den Taschenrechner die Funktion
\( \quad f(x) = 2x^3 - 18 x^2 + 28x + 48 \)
\(\\\)
mit dem Tabellenbereich

\(\\\)
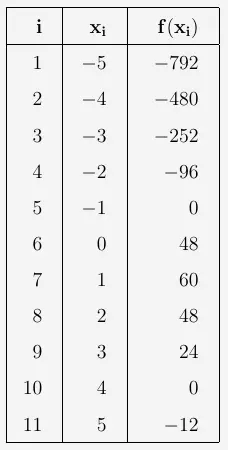
ein. Folgende Wertetabelle wird angezeigt:
\(\\\)
Wir wählen \(x_1=4\). Nun legen wir eine Tabelle an mit den Parametern des Funktionsterms
\( \quad 2x^3 - 18 x^2 + 28x + 48 \)
\(\\\)
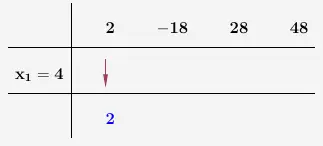
in der Kopfzeile. Wir ziehen den 1. Parameter nach unten.
\(\\\)
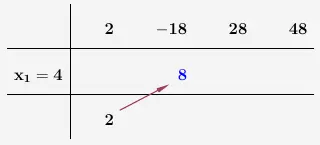
Wir rechnen diese Zahl, hier die \(2\), mal den \(x\)-Wert und setzen das Ergebnis in die mittlere Zeile.
\(\\\)
Nun addieren wir die beiden übereinander stehenden Zahlen und schreiben das Ergebnis in die untere Zeile.

\(\\\)
Das Ergebnis wird wieder mal den \(x\)-Wert gerechnet und in die mittlere Zeile geschrieben. Die übereinander stehenden Zahlen werden addiert und das Ergebnis darunter notiert.

\(\\\)
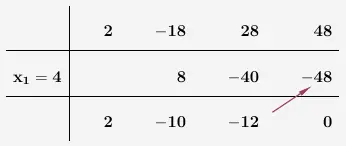
Und das Ganze ein letztes Mal.
\(\\\)
Die letzte Zeile ist nun so zu lesen:
\( \quad 2 x^2 - 10x - 12 = 0 \)
\(\\\)
Das heißt, um die Bezug zur ursprünglichen Aufgabe wieder herzustellen, können wir jetzt schreiben:
\( \quad \begin{array}{ r c l } 0 & = & (x-4) \cdot \left(2 x^2 - 10x - 12\right) \\[6pt] 0 & = & 2x^3 - 18 x^2 + 28x + 48 \\ \end{array} \)
\(\\\)
Wir brauchen also nur
\( \quad 0 = 2 x^2 - 10x - 12 \)
\(\\\)
lösen, um auch die restlichen Nullstellen zu bekommen. Das machen wir mit der PQ-Formel. Zunächst teilen wir durch \(2\).
\( \quad 0 = x^2 - 5x - 6 \)
\(\\\)
Weiter geht es mit der Lösungsformel.
\( \quad \begin{array}{ r c l } x_{2,3} & = & -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q} \\[8pt] x_{2,3} & = & -\frac{-5}{2}\pm \sqrt{\left(\frac{-5}{2}\right)^2-(-6)} \\[8pt] x_{2,3} & = & \frac{5}{2}\pm \sqrt{\frac{25}{4} +6} \\[8pt] x_{2,3} & = & \frac{5}{2}\pm \sqrt{\frac{25}{4} +\frac{24}{4}} \\[8pt] x_{2,3} & = & \frac{5}{2} \pm \sqrt{\frac{49}{4}} \\[8pt] x_{2,3} & = & \frac{5}{2}\pm \frac{\sqrt{49}}{\sqrt{4}} \\[8pt] x_{2,3} & = & \frac{5}{2}\pm \frac{7}{2} \\[6pt] x_2 & = & 6 \\[6pt] x_3 & = & -1 \\ \end{array} \)
\(\\[1em]\)