Symmetrie
Inhaltsverzeichnis
\(\\\)
Was sind symmetrische Darstellungen?
Das sind Darstellungen, die eine gewisse Art von Regelmäßigkeiten aufweisen.
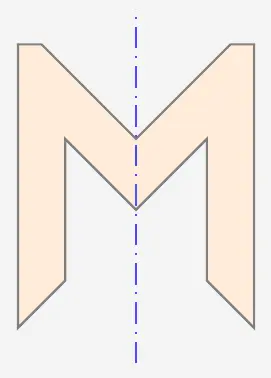
Zum einen können es Darstellungen sein, in die man eine Symmetrieachse so legen kann, dass die eine Seite der Darstellung auf der anderen Seite der Symmetrieachse spiegelbildlich erscheint. Bei dem Buchstaben \(M\) handelt es sich also um eine Achsensymmetrie.
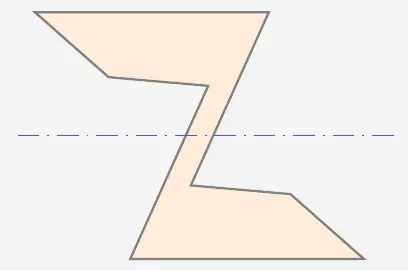
\(\\\) Betrachten wir nun den Buchstaben \(Z\). Dieser scheint auch irgendwie symmetrisch zu sein, aber nicht wie bei dem Buchstaben \(M\). Denn wie wir hier die Symmetrieachse auch anlegen, würden die Darstellung jenseits der Symmetrieachse immer verkehrt herum liegen.
\(\\\)
Betrachten wir die Darstellung jedoch von einem Zentrumspunkt aus, so kann die Regelmäßigkeit erfasst werden.
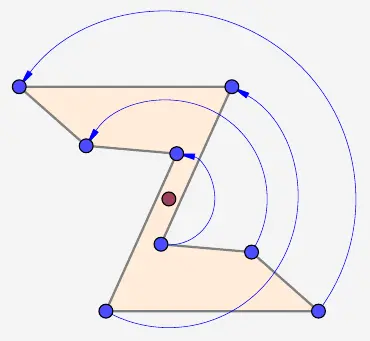
Denn von diesem Punkt aus sind alle Punkte um 180° gedreht in der Darstellung vorhanden. Es handelt sich also um eine Drehsymmetrie (oder auch Punktsymmetrie).
\(\\[1em]\)
1. Achsensymmetrie
Bezogen auf Funktionen und ihre Graphen handelt es sich bei der Achsensymmetrie um eine Symmetrie um die \(y\)-Achse. Daraus ergibt sich, dass der Graph von \(f(x)\) um die \(y\)-Achse gespiegelt den gleichen Graphen wie von \(f(-x)\) ergibt.
Es folgt damit die Bedingung
\(\quad f(x) = f(-x) \)
\(\\\)
Das heißt, dass alle positiven \(x\)-Werte und die entsprechenden negativen \(x\)-Werte denselben \(y\)-Wert haben.
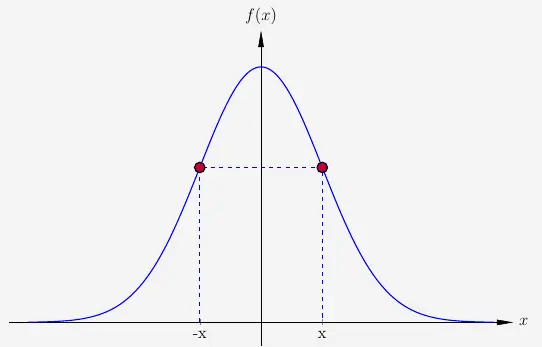
Hier liegt nun die Gauß'sche Glockenkurve vor mit
\( \quad f(x) = \frac{1}{\sqrt{2 \cdot \pi}}\cdot e^{-\frac{1}{2} \cdot x^2} \)
\(\\\)
Wir überprüfen die Achsensymmetrie, indem wir \(f(-x)\) bestimmen.
\( \quad f(-x) = \frac{1}{\sqrt{2 \cdot \pi}} e^{-\frac{1}{2} \cdot (-x)^2} = \frac{1}{\sqrt{2 \cdot \pi}} e^{-\frac{1}{2} \cdot x^2} \)
Die Funktionsgleichungen sind nach dem Auflösen identisch und damit ist die Bedingung für alle Punkte der Funktion erfüllt und die Achsensymmetrie nachgewiesen.
\(\\[2em]\)
2. Punktsymmetrie
Eine Punktsymmetrie (Drehsymmetrie) hat bei Funktionen als Zentrumspunkt den Koordinatenursprung. Eine Drehung einer Funktion um den Ursprung können wir erreichen indem wir die Funktion sowohl um die \(x\)-Achse als auch um die \(y\)-Achse spiegeln.
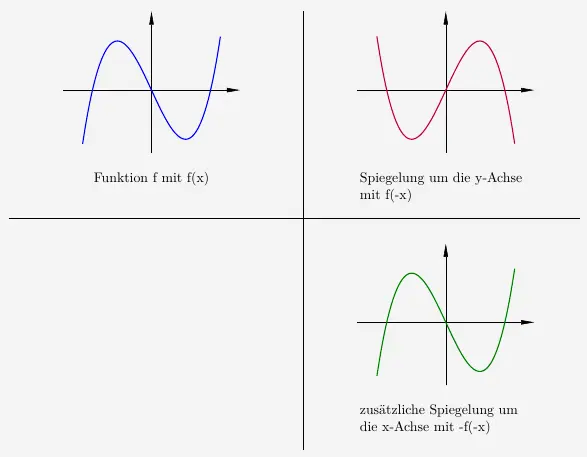
Wir können erkennen, dass der Graph von der punktsymmetrischen Funktion \(f\) und seine zweifache Spiegelung identisch sind. Es gilt also bei einer Punktsymmetrie die Bedingung
\( \quad f(x) = -f(-x) \)
\(\\\)
Wir überprüfen das rechnerisch an der obigen Funktion \(f\).
\( \quad \begin{array}{ r c l } f(x) & = & x^3 - 9x \\[15pt] -f(-x) & = & - \left((-x)^3 - 9 \cdot (-x)\right) \\[6pt] -f(-x) & = & - \big((-x) \cdot (-x) \cdot (-x) - 9 \cdot (-x)\big) \\[6pt] -f(-x) & = & - \left(-x^3 + 9 x \right) \\[6pt] -f(-x) & = & x^3 - 9 x \\[6pt] -f(-x) & = & f(x) \\ \end{array} \)
\(\\\)
Alternativ kann eine Punktsymmetrie auch nachgewiesen werden durch die Tatsache, dass eine punktsymmetrische Funktion um die \(x\)-Achse gespiegelt den gleichen Graphen ergibt wie eine um die \(y\)-Achse gespiegelte Funktion.
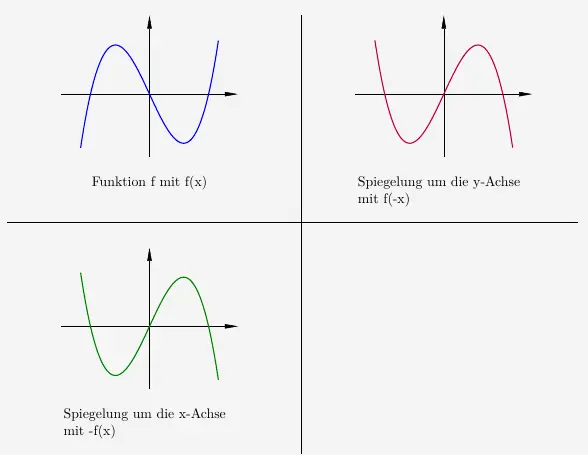
\(\\\)
Es gilt also ebenso die Bedingung
\( \quad f(-x) = -f(x) \)
\(\\\)
Auch das können wir rechnerisch anhand der Funktion \(f\) nachweisen.
\( \quad \begin{array}{ r c l } f(-x) & = & (-x)^3 - 9 \cdot (-x) \\[6pt] f(-x) & = & (-x) \cdot (-x) \cdot (-x) - 9 \cdot (-x)\\[6pt] f(-x) & = & -x^3 + 9 x \\[15pt] -f(x) & = & -\left( x^3 - 9 x \right) \\[6pt] -f(x) & = & -x^3 + 9 x \\[6pt] -f(x) & = & f(-x) \\ \end{array} \)
\(\\[2em]\)
3. Symmetriebestimmung ganzrationaler Funktionen
Betrachten wir die Potenzfunktionen mit gerade Exponenten,
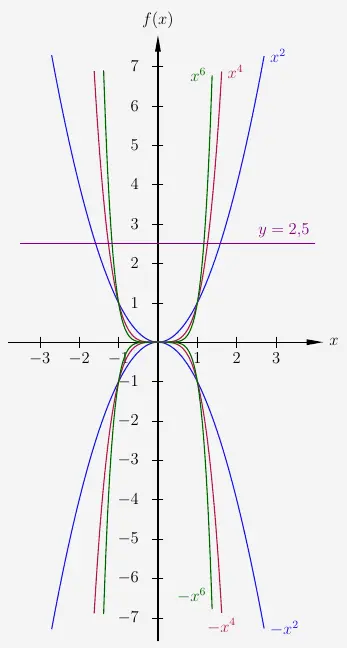
so ist zu erkennen, dass alle achsensymmetrisch sind. Also gilt auch für Polynome, also ganzrationale Funktionen, dass diese achsensymmetrisch sind, wenn sie nur Potenzfunktionen mit geraden Exponenten enthalten. Wie oben zu sehen ist, sind auch konstante Funktionen vom Typ
\( \quad f(x) = c \; , \quad c \in \mathbb{R} \)
\(\\\)
achsensymmetrisch. Achsensymmetrische Funktionen können Konstanten enthalten wie zum Beispiel
\( \quad f(x) = 0{,}5x^4 - 3x^2 + 2 \)
\(\\\)
Wie in diesem Beispiel können die Potenzfunktionen auch gestreckt oder gestaucht vorliegen.
\(\\\) Entsprechend gilt bei ganzrationalen Funktionen, die nur Potenzfunktionen mit ungeraden Exponenten
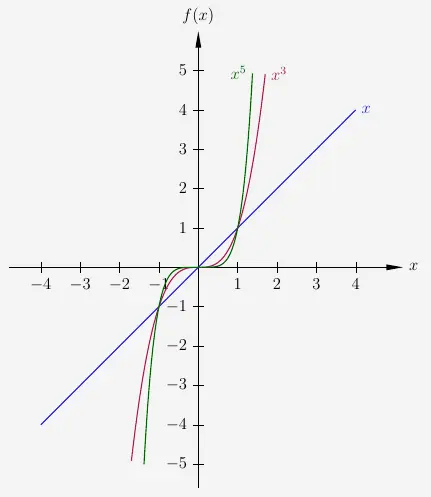
enthalten, stets punktsymmetrisch sind.
Beachte:
Punktsymmetrische Funktionen dürfen keine Konstanten enthalten, da diese ja achsensymmetrisch sind.
\(\\[2em]\)
4. Symmetrieuntersuchung zusammengesetzter Funktionen
Für zusammengesetzte Funktionen folgen 2 Beispiele einer vollständigen Symmetrieuntersuchung:
\(\\\)
Beispiel 1 :
\( \quad f(x)=\frac{8x}{e^{x^2}} \)
\(\\\)
Wir untersuchen zunächst die Achsensymmetrie mit
\( \quad f(x) = f(-x) \)
\(\\\)
und bilden
\( \quad \begin{array}{ r c l } f(-x) & = & \frac{8 \cdot (-x)}{e^{(-x)^2}} \\[8pt] f(-x) & = & \frac{-8x}{e^{x^2}} \\[8pt] f(-x) & = & -\frac{8x}{e^{x^2}} \\ \end{array} \)
\(\\\)
Diese Funktion ist nicht achsensymmetrisch, denn \(f(x) \not= f(-x)\). Weiter untersuchen wir die Punktsymmetrie mit der Bedingung
\( \quad f(x) = -f(-x) \)
\(\\\)
und bilden
\( \quad \begin{array}{ r c l } -f(-x) & = & -\left(-\frac{8x}{e^{x^2}}\right) \\[8pt] -f(-x) & = & \frac{8x}{e^{x^2}} \\[8pt] -f(-x) & = & f(x) \\ \end{array} \)
\(\\\)
Die Bedingung der Punktsymmetrie ist für alle \(x\)-Werte erfüllt.
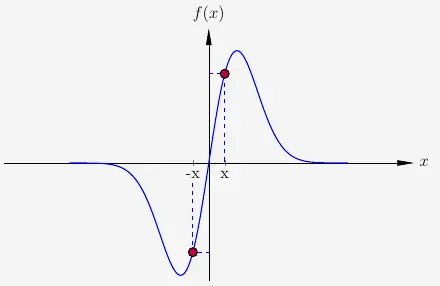
\(\\\)
Beispiel 2 :
Wir beginnen wieder mit der Achsensymmetrie und bestimmen von der Funktion \(f\) mit
\( \quad f(x)=\left( 10 x + 10x^4 \right) \cdot e^{x^3} \)
\(\\\)
den Funktionsterm für \(f(-x)\) :
\( \quad \begin{array}{ r c l } f(-x) & = & \left( 10 \cdot (-x) + 10 \cdot (-x)^4 \right) \cdot e^{(-x)^3} \\[5pt] f(-x) & = & \left( -10x + 10 \cdot (-x) \cdot (-x) \cdot (-x) \cdot (-x)\right) \cdot e^{(-x) \cdot (-x) \cdot (-x)} \\[5pt] f(-x) & = & \left( -10x + 10 \cdot x^4 \right) \cdot e^{-x^3} \\[5pt] f(-x) & \not= & f(x) \\ \end{array} \)
\(\\\)
Diese Funktion ist nicht achsensymmetrisch. Weiter überprüfen wir die Punktsymmetrie dieses Mal mit der Bedingung
\( \quad f(-x) = -f(x) \)
\(\\\)
Wir benötigen \(-f(x)\) :
\( \quad \begin{array}{ r c l } -f(x) & = & -\left( 10 x + 10x^4 \right) \cdot e^{x^3} \\[6pt] -f(x) & = & \left( -10 x - 10x^4 \right) \cdot e^{x^3} \\[6pt] -f(x) & \not= & f(-x)\\ \end{array} \)
\(\\\)
Damit ist die Funktion weder achsen- noch punktsymmetrisch, also insgesamt nicht symmetrisch.
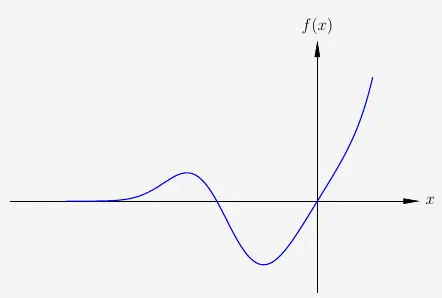
\(\\[1em]\)