Extrempunkte der Schar
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Ortsgerade der Extrempunkte
Eine Gerade, auf der alle Extrempunkte einer Funktionenschar liegen, nennt man die Ortsgerade der Extrempunkte. Wie wird diese nun ermittelt? Zunächst benötigen wir die Extrempunkte.
\(\\\)
Extrempunkte
Es gilt die notwendige Bedingung: \(h'(x) =0\)
Wir definieren die erste Ableitung

\(\\\)
und berechnen die Gleichung.

\(\\\)
Mit
\( \quad x_1 \; = \; -\frac{1}{\sqrt{a}} \quad \textit{und} \quad x_2 \; = \; \frac{1}{\sqrt{a}} \)
\(\\\)
existieren nur Extrempunkte mit der Voraussetzung \(a > 0\), denn der Wurzelinhalt muss größer gleich Null sein und der Nenner darf nicht Null ergeben.
Weiter gilt die hinreichende Bedingung: \(h''(x) \not= 0\)
Wir bilden die zweite Ableitung

\(\\\)
und überprüfen die Lösungen.

\(\\\)
Es folgt
\( \quad \begin{array}{ r c r c c c l } h''(x_1) & = & 2 \cdot \sqrt{a} & > & 0 & \quad \Rightarrow & \textit{Tiefpunkt} \\[8pt] h''(x_2) & = & -2 \cdot \sqrt{a} & < & 0 & \quad \Rightarrow & \textit{Hochpunkt} \\ \end{array} \)
\(\\\)
Mit den Funktionswerten

\(\\\)
ergeben sie die Tiefpunkte \(\left(-\frac{1}{\sqrt{a}} \Bigl| -\frac{1}{\sqrt{a}} \right)\) und die Hochpunkte \(\left(\frac{1}{\sqrt{a}} \Bigl| \frac{1}{\sqrt{a}} \right)\) der Schar.
\(\\[1em]\)
Ortsgerade
Mit den Hochpunkten der Schar ist
\( \quad \begin{array}{ r c r c l } \textrm{I} && x & = & \frac{1}{\sqrt{a}} \\[8pt] \textrm{II} && y & = & \frac{1}{\sqrt{a}} \\ \end{array} \)
\(\\\)
Zur Bestimmung der Ortsgeraden wird nun folgendermaßen vorgegangen:
-
\(x\) nach \(a\) auflösen:
\( \quad \begin{array}{ r c l l } x & = & \frac{1}{\sqrt{a}} & \bigl| \, \cdot \sqrt{a} \\[6pt] \sqrt{a} \cdot x & = & 1 & \bigl| \, : x \\[6pt] \sqrt{a} & = & \frac{1}{x} & \bigl| \, (\dots)^2 \\[6pt] a & = & \frac{1}{x^2} & \\ \end{array} \)
\(\\\)
-
\(a\) in \(y\) einsetzen:
\( \quad \begin{array}{ r c l } y & = & \dfrac{1}{\frac{1}{\sqrt{x^2}}} \\[8pt] y & = & \dfrac{1}{\frac{1}{x}} \\[8pt] y & = & 1 : \frac{1}{x} \quad \text{Bruchrechenregel anwenden!} \\[8pt] y & = & 1 \cdot\frac{x}{1} \\[6pt] y & = & x \\ \end{array} \)
\(\\\)
Verwenden wir statt den Koordinaten der Hochpunkte die der Tiefpunkte, so führt dies zum gleichen Ergebnis.
Die Gleichung
\( \quad y \; = \; x \)
ist die Ursprungsgerade mit der Steigung \(m=1\).

\(\\[2em]\)
Aufgabe 2 – Viereck mit Flächeninhalt von 144

\(\\\)
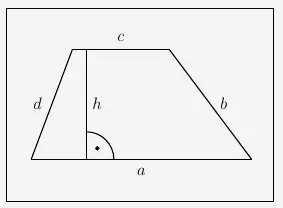
Das eingezeichnete Viereck stellt ein gedrehtes Trapez
\(\\\)
dar. Für Trapeze gilt die Flächenformel
\( \quad A = \dfrac{a + c}{2} \cdot h \)
\(\\\)
Wie aus der voherigen Aufgabe hervorgeht, liegen alle Hochpunkte bei \(\left(\frac{1}{\sqrt{a}} \Bigl| \frac{1}{\sqrt{a}}\right)\). Daraus ergeben sich folgende Werte für die Trapezformel:
\( \quad \begin{array}{ r c c } a & = & \frac{1}{\sqrt{a}} \\[8pt] c & = & 2 \\[6pt] h & = & \frac{1}{\sqrt{a}} \\ \end{array} \)
\(\\\)
Eingesetzt in die Formel ergibt sich nun folgende Gleichung:
\( \quad 144 = \dfrac{\frac{1}{\sqrt{a}} + 2}{2} \cdot \dfrac{1}{\sqrt{a}} \)
\(\\\)
Wir lösen die Gleichung mit dem CAS.

\(\\\)